Exercice 1 tp

1) Résoudre dans IR l'équation
(E): tanx=√3.
2) Déterminer les solutions de (E) sur l'intervalle I=[-π;π].
3) Représenter les solutions de (E) sur le cercle trigonométrique (C).

Correction

Rappel

D= IR \ {	π	+ kπ / k∈ℤ}
	2

1) Pour tout x∈D on a tan(x+π)=tan(x).
2) x≡y[π] signifie x=y+kπ (k∈ℤ).

Soit x∈I. tanx∈IR si

x≠	-π	et x≠	π
	2		2

On a

tan(	π	) = √3
	3

donc (E) signifie

tanx = tan(	π	)
	3

signifie

x =	π	+kπ (k∈ℤ)
	3

2) On encadre ces solutions
dans l'intervalle I=[-π;π]

-π≤	π	+kπ	≤π
	3

signifie

-1≤	1	+k	≤1
	3

Signifie

-1-	1	≤+k≤1-	1
	3		3

signifie

-4	≤k≤	2
3		3

k∈ℤ donc k=-1 ou k=0 ainsi

x =	π	ou x =	-2π
	3		3

Ces deux solutions sont toutes les deux différentes de

-π	et	π
2		2

alors l'ensemble des solutions de (E)

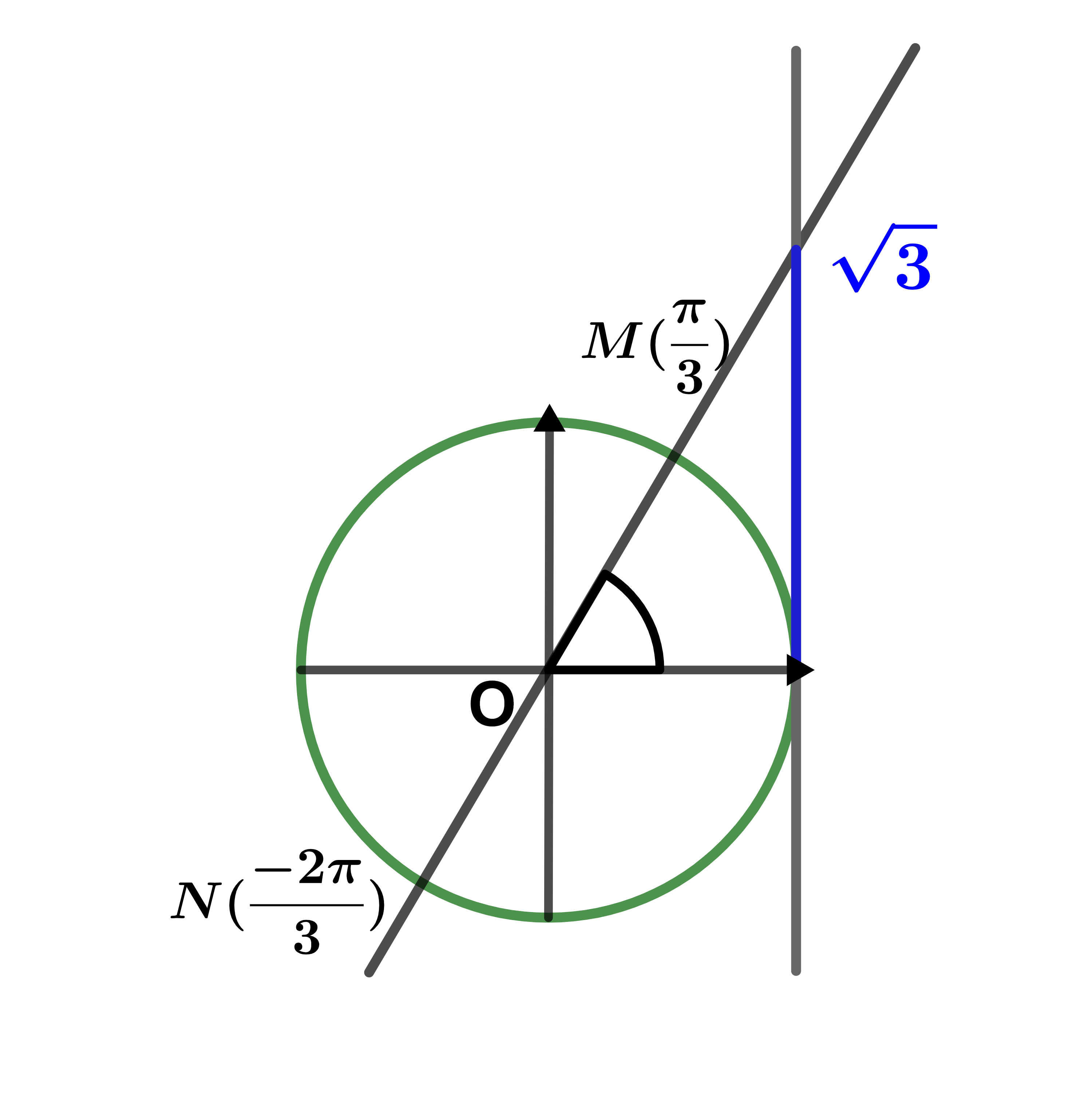
S = {	-2π	;	π	}
	3		3

Représentation des solutions sur le cercle trigonométrique.

Exercice 2 tp

1) Résoudre dans IR l'équation
(E): tanx=-√3.
2) Déterminer les solutions de (E) sur l'intervalle I=[0;3π].
3) Représenter les solutions de (E) sur le cercle trigonométrique (C).