تمرين 1 tp
حل في المجال I=[-π;π] المعادلة
(E):2cosx=√2.
تصحيح
اولا نحل المعادلة (E) في IR
المعادلة (E) تكافئ
| أو |
x = |
π |
+2kπ/ k∈ℤ |
اذن |
| 4 |
| x =- |
π |
+2k'π/ k'∈ℤ |
| 4 |
ثانيا نؤطر هذه الحلول في المجال I=[-π;π]
| x2 = |
-π |
اذن k'=0 فان k'∈ℤ |
| 4 |
| S = { |
π |
; |
-π |
} ومنه فان |
| 4 |
4 |
ملاحظة هنا ..
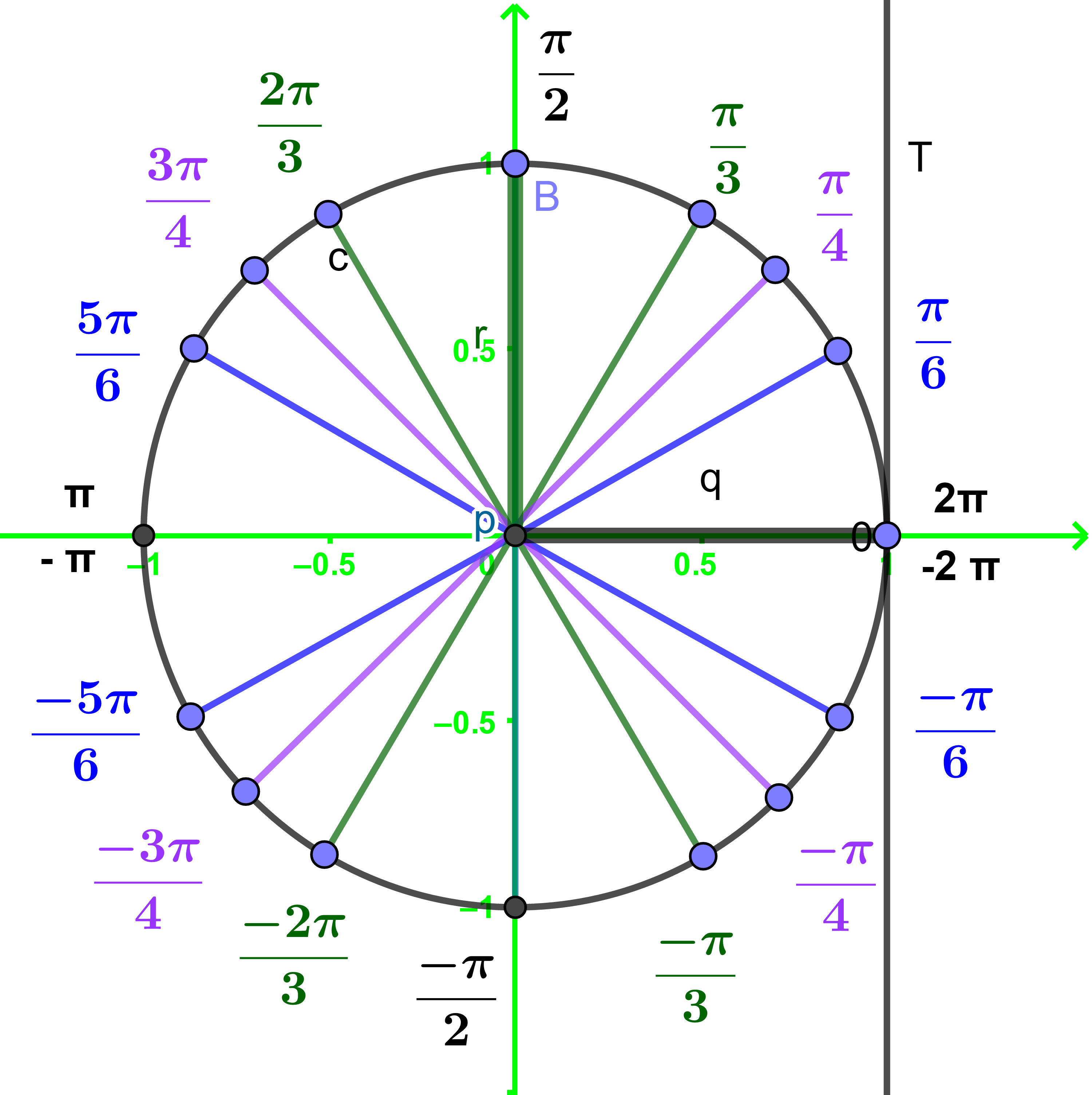
باستعمال الدائرة المثلثية (C)
الحلان الوحيدان في المجال I هما
تمرين 2 tp
حل في المجال I=[-π;π] المعادلة
(E): 2cosx+√2=0.
تصحيح
اولا نحل المعادلة (E) في IR
| cos( |
3π |
) = - |
√2 |
لدينا |
| 4 |
2 |
| أو |
x = |
3π |
+2kπ/ k∈ℤ |
اذن |
| 4 |
| x = - |
3π |
+2k'π/ k'∈ℤ |
| 4 |
ثانيا نؤطر هذه الحلول في المجال I=[-π;π]
| 3π≤ |
2π |
+2kπ |
≤π |
(a) |
| 4 |
| -1≤ |
3 |
+2k |
≤1 |
يعني |
| 4 |
| x1 = |
3π |
اذن k=0 فان k∈ℤ |
| 4 |
| x2 = |
-3π |
اذن k'=0 فان k'∈ℤ |
| 4 |
| S = { |
-3π |
; |
3π |
} ومنه فان |
| 4 |
4 |
ملاحظة هنا ..
باستعمال الدائرة المثلثية (C),
الحلان الوحيدان في المجال I هما