تمرين 1 tp

1) حل في IR المعادلة
(E): tanx=√3.
2) حل في I=[-π;π] المعادلة (E)
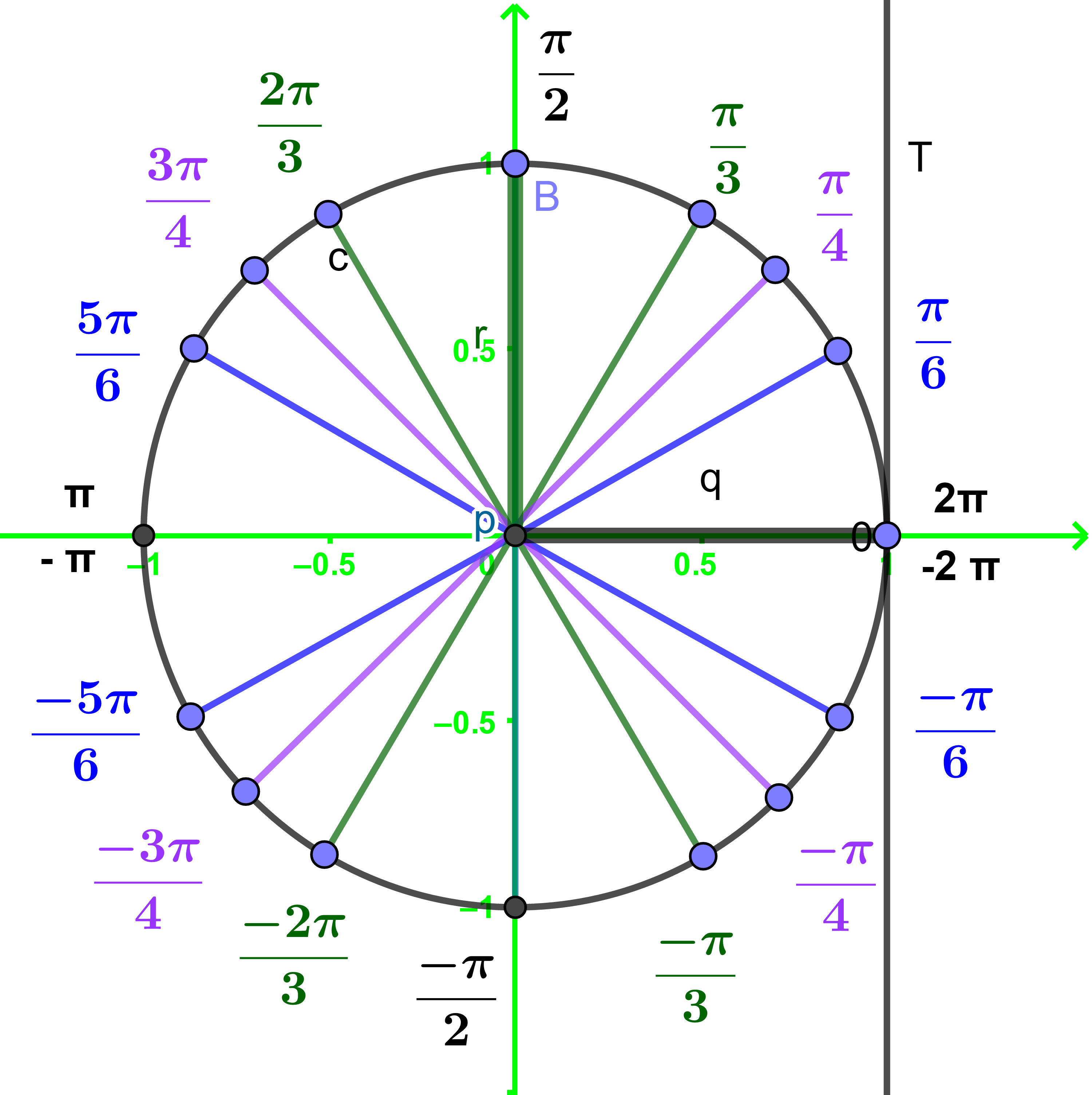
3) مثل حلول المعادلة (E) على الدائرة المثلثية.

تصحيح

D= IR \ {	π	+ kπ / k∈ℤ}
	2

1) لكل x∈D لدينا tan(x+π)=tan(x).
2) x≡y[π] يعني x=y+kπ (k∈ℤ).

ليكن x∈I. tanx∈IR اذا كان

x≠	-π	و x≠	π
	2		2

tan(	π	) = √3	لدينا
	3

اذن (E) تعني

tanx = tan(	π	)
	3

x =	π	+kπ/ k∈ℤ اذن
	3

ثانيا نؤطر هذه الحلول في المجال I=[-π;π].

-π≤	π	+kπ	≤π لدينا
	3

-1≤	1	+k	≤1 يعني
	3

-1-	1	≤+k≤1-	1	يعني
	3		3

-4	≤k≤	2	يعني
3		3

بما ان k∈ℤ فان k=-1 او k=0 ومنه فان

x =	π	او x =	-2π
	3		3

هذه الحلول مختلفة عن

-π	و	π
2		2

وبالتالي مجموعة حلول المعادلة (E)

S={	-2π	;	π	}
	3		3

تمرين 2 tp

1) حل في IR المعادلة
(E): tanx= -√3.
2) حل في I=[0;3π] المعادلة (E)
3) مثل حلول المعادلة (E) على الدائرة المثلثية.