تمرين 1 tp

حل في [0;π]
المتراجحة 2cosx≥1.

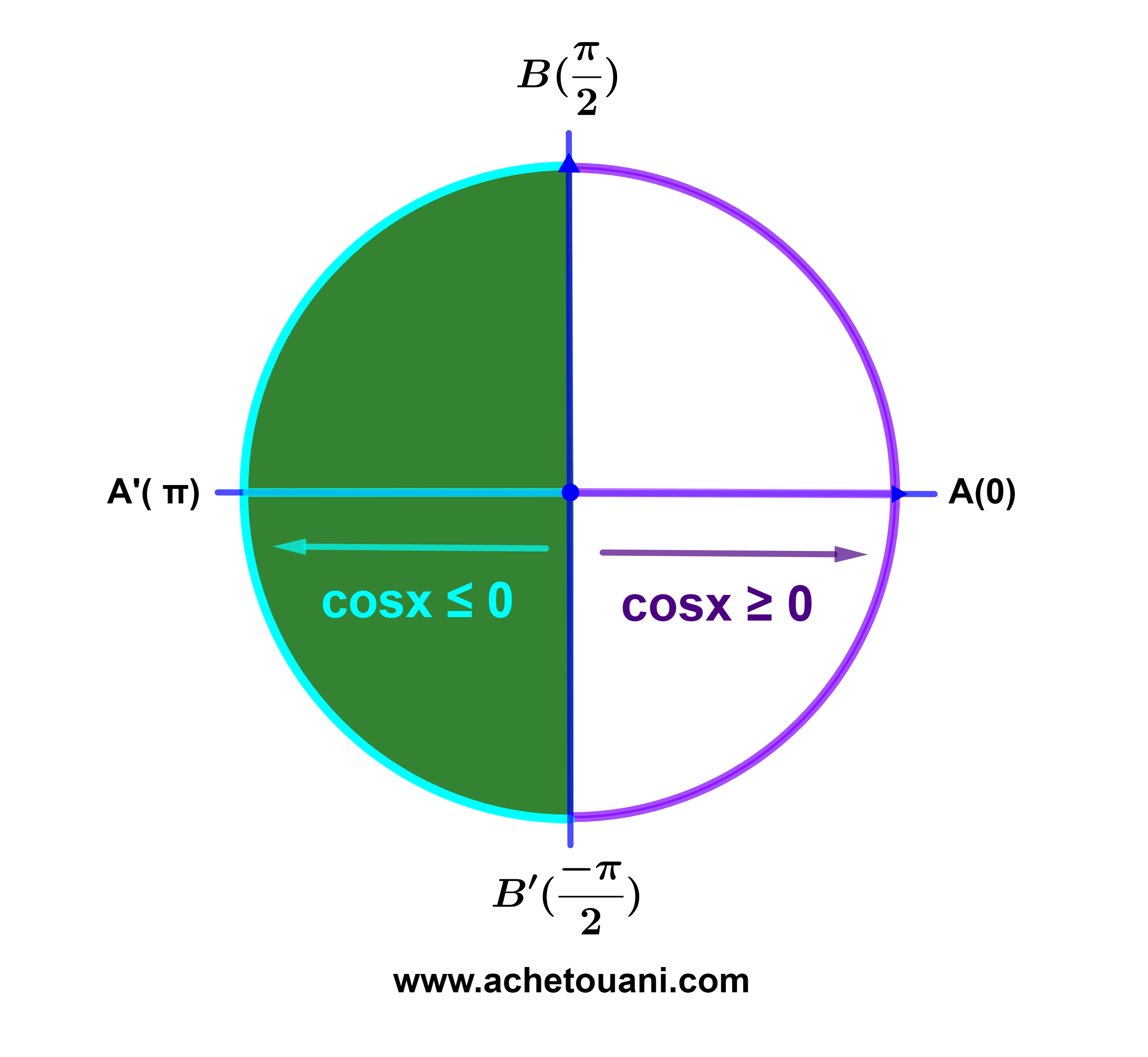
تذكير

x∈[	-π	;	π	] اذا كان
	2		2

فان cosx≥0.

x∈[-π;	-π	] ∪ [	π	; π] اذا كان
	2		2

فان cosx≤0.

بصفة عامة

x∈[	-π	+2kπ ;	π	+2kπ]	اذا كان	(1
	2		2

فان cosx≥0.

x∈[-π+2kπ ;	-π	+2kπ]	اذا كان	(2
	2

فان cosx≤0.

x∈ [	π	+2kπ ; π+2kπ]	اذا كان	(3
	2

فان cosx≤0.

تصحيح

1) نحل المعادلة
(E) 2cosx=1 في IR.

cosx =	1	تعني	(E)
	2

لدينا

cos(	π	)=	1
	3		2

أو	x =	π	+2kπ	k و k'∈ℤ
		3
	x = -	π	+2k'π
		3

2) نؤطر الحلول في المجال I

0 ≤	π	+ 2kπ	≤ π	(a)
	3

0 ≤	1	+2 k	≤ 1
	3

-	1	≤ + 2k≤ 1 -	1	يعني
	3		3

-1	≤k≤	2	يعني
6		6

k∈ℤ اذن k=0

x =	π	+2kπ	(k∈ℤ) لدينا
	3

x =	π	اذن
	3

0 ≤	-π	+ 2k'π	≤ π	(b)
	3

يعني

0 ≤	-1	+ 2k'	≤ 1
	3

يعني

0 +	1	≤ 2k'≤ 1 +	1
	3		3

يعني

1	≤ k' ≤	4
6		6

k'∈ℤ اذن قيمة k' غير موجودة
3) نمثل هده الحلول على محور أو على الدائرة المثلثية (C).
(0)----(π/3)----(π/2)----(π)

S = [0 ;	π	]
	3