تمرين 1 tp

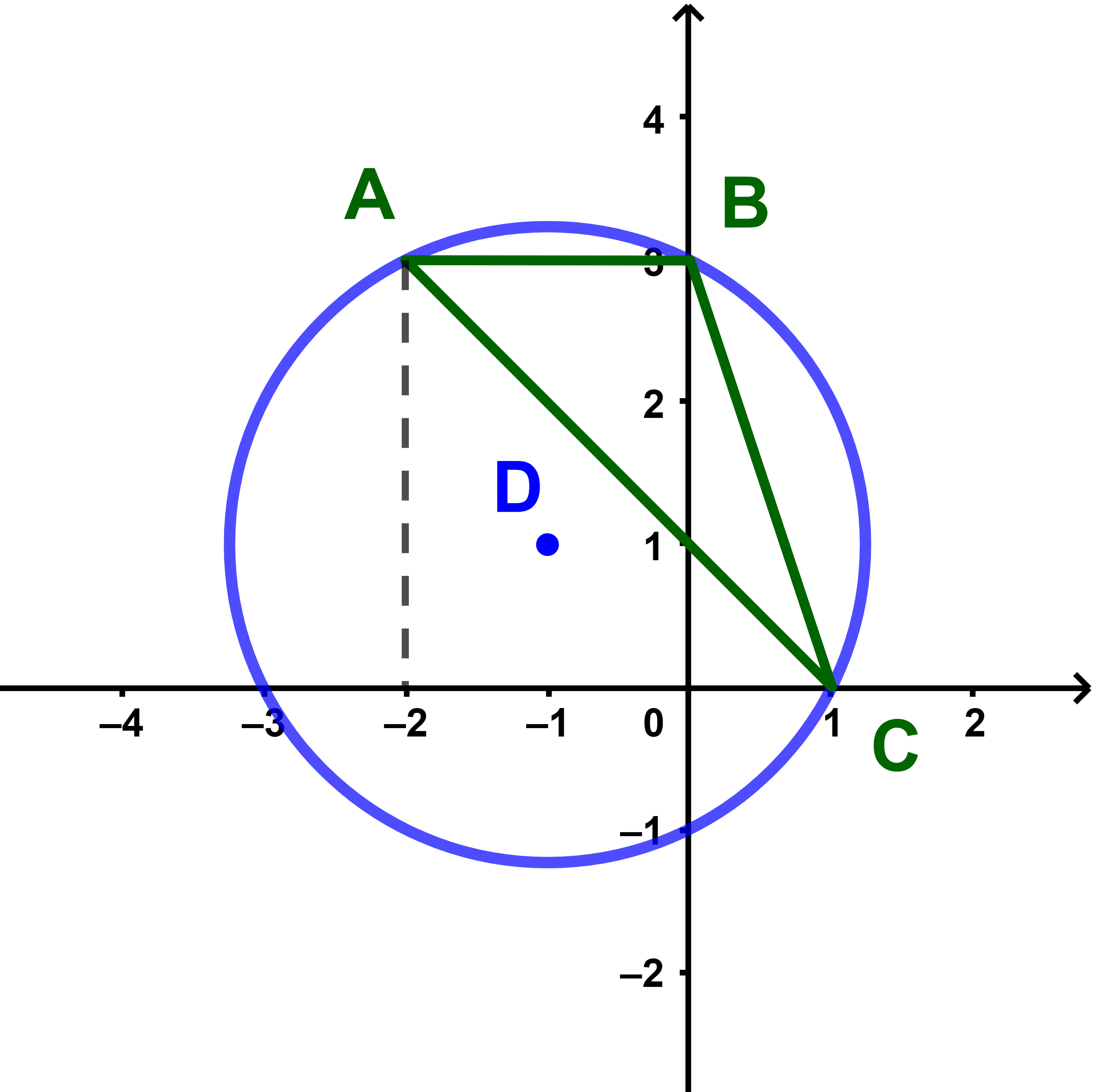
المستوى ℙ منسوب الى معلم متعامد ممنظم (O;i^→;j^→) . نعتبر في ℙ النقط A(-2;3) و B(0;3) و C(1;0) و D(-1;1).
1) مثل النقط في المعلم النقط A و B و C و D.
2) بين أن D مركز الدائرة المحيطة بالمثلث (ABC).

3) ما هي طبيعة المثلث (DBC)?
4) احسب قياس الزاوية (AC;AB)?

تمرين 2 tp

1) نعتبر الدائرة التالية

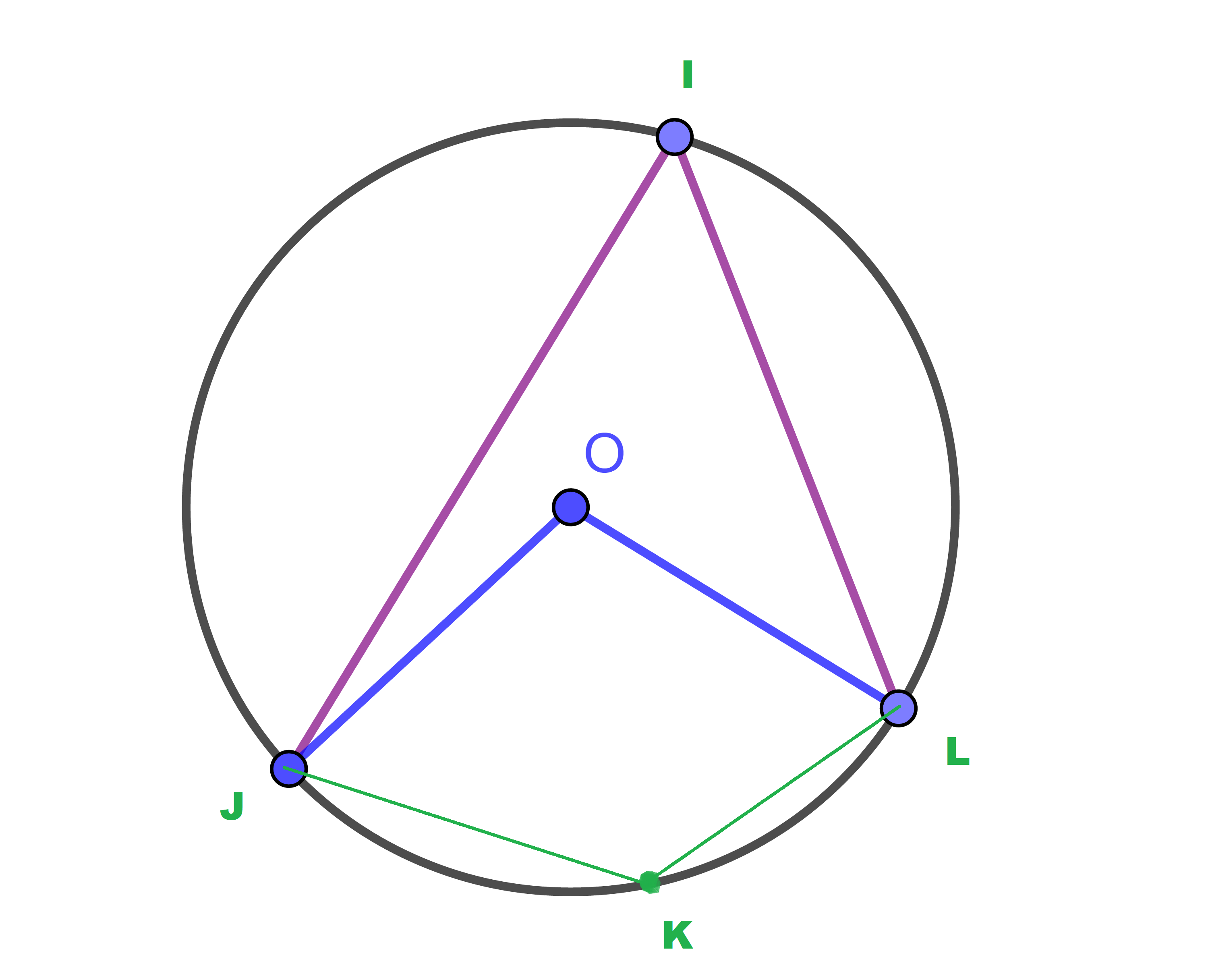
اذا كان [LOJ]=110°
حدد قيمة الزاوية [JKL].

2) لتكن A و B و C و D نقط الدائرة المثلثية التي مركزها O بحيث القوسان arc(AB) و arc(CD) لهما نفس القياس ونصفي المستقيمان [AB) و [CD) متقاطعان في النقطة E.
انشئ الشكل وبين أن النقط O و B و E و D متداورة.

تصحيح

1) لدينا [LOJ]=2[LIJ] والرباعي IJKL متداور
اذن [LIJ]+[JKL]=π=180°
ولدينا [JKL]=180°-55°=125° .

تذكير الرباعي OBED متداور يعني
[DOB]+[BED]=π=180°.
أو
[EDO]+[OBE]=π=180° .

2) نستعمل لهذا السؤال
[EDO]+[OBE]=π=180°

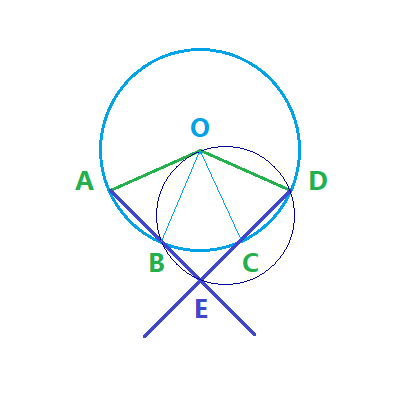
نضع x= [EDO] و y=[OBE]
(a) OD=OC اذن المثلث OCD متساوي الساقين رأسه O
ومنه فان 2x+[DOC]=π (العلاقة 1).
(b) OA=OB اذن المثلث OAB متساوي الساقين رأسه O
اذن 2[ABO]+[BOA]=π
وبما أن arc(AB)=arc(CD)
فان [BOA]=[DOC].
لدينا اذن 2[ABO]+[BOA]=π
يعني 2[ABO]+[DOC]=π (العلاقة 2).

من العلاقتين (1) و (2) نستنتج
2x+[DOC] = 2[ABO]+[DOC]
يعني x=[ABO]
لدينا [ABO]+[OBE]=π
اذن x+y=π وهذا يعني أن OBED متداور أي النقط O و B و E و D متداورة.