1.3.2 Extremums d'une fonction dérivable

Définition 1 Soit f une fonction dérivable sur un intervalle I. La plus petite valeur des images des éléments de l'intervalle I par f est appelée valeur minimale de f.
En d'autre terme
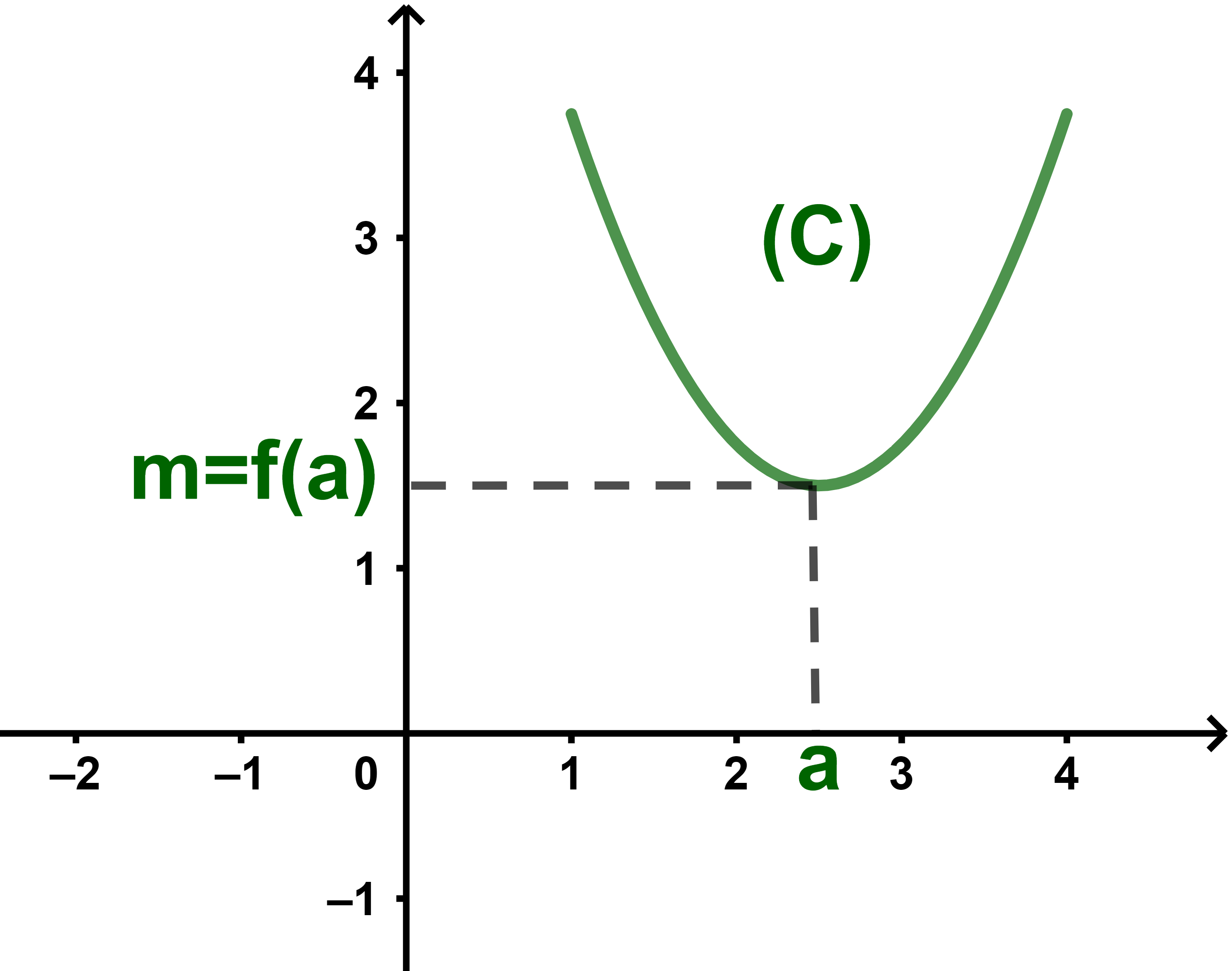
m est une valeur minimale de f signifie qu'il existe un nombre réel a de I
tel que ∀x∈I) f(x)≥f(a)=m.

Définition 2 Soit f une fonction dérivable sur un intervalle I. La plus grande valeur des images des éléments de l'intervalle I par f est appelée valeur maximale de f.
En d'autre terme
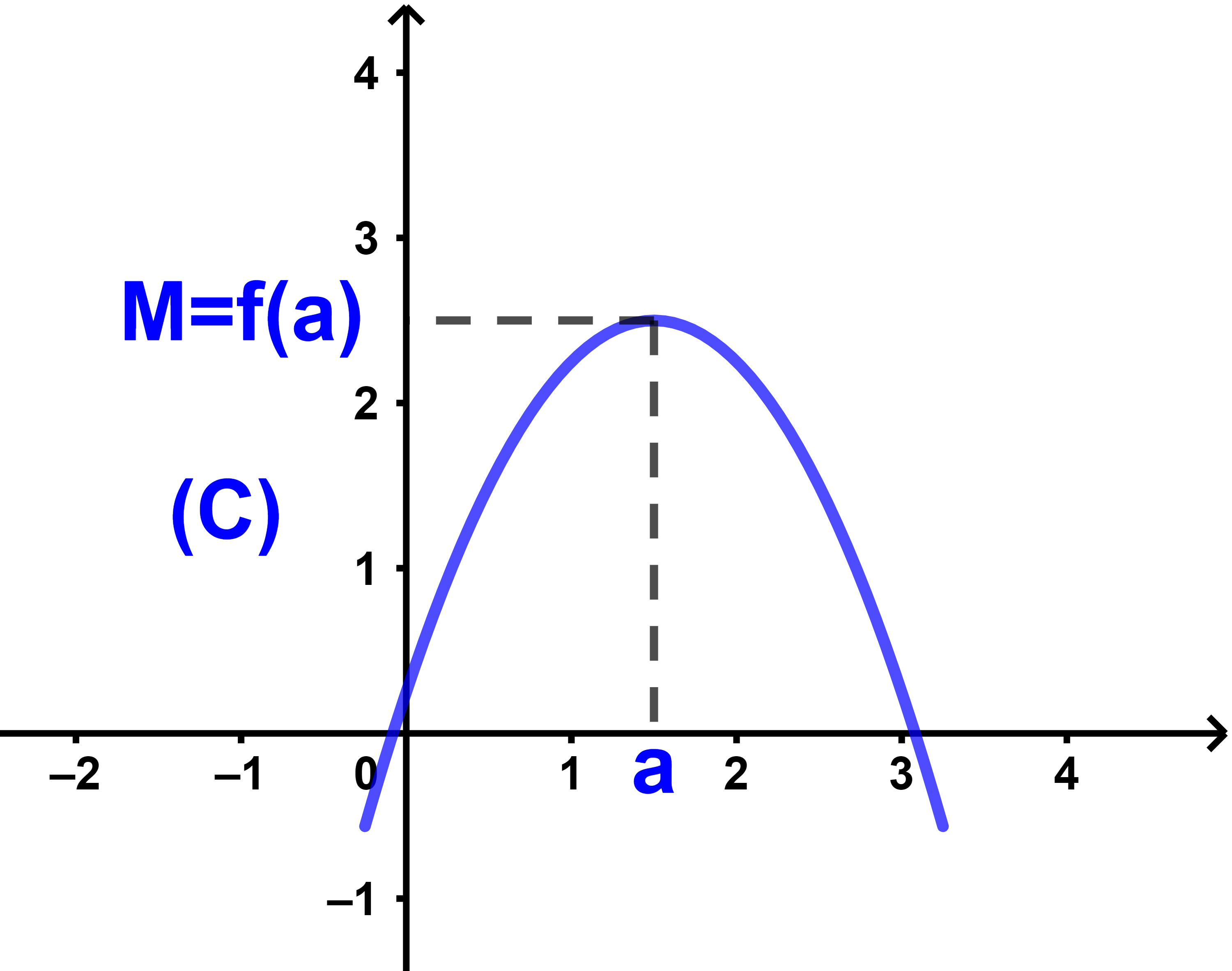
M est une valeur maximale de f signifie qu'il existe un nombre réel a de I
tel que ∀x∈I) f(x)≤f(a)=M.

Définition 3 Soit f une fonction définie sur un intervalle I et a∈I.
On dit que f(a) est un extremum de f sur I si f(a) est une valeur minimale ou valeur maximale sur I.

Propriété 1 Soit f une fonction dérivable sur un intervalle I et a∈I.
Si f admet un extrémum au point a alors f'(a)=0.

Remarque
La réciproque de la Propriété 1 n'est pas toujour vraie.
Exemple Soit f une fonction définie par f(x)=x³.
On a f'(x)=3x² donc f'(0)=0
mais f n'admet pas un extremum au point 0
car 0 n'est pas une valeur minimale et non plus une valeur maximale.

Propriété 2 Soit f une fonction dérivable sur un intervalle I et a∈I.
Si f' s'annule au point a (c'est à dire f'(a)=0) et change de signe au voisinage de a alors f(a) est un extremum de f.