1.3 المقارب الموازي لمحور الافاصيل

1.3.1 تعاريف

لتكن f دالة عددية لمتغير حقيقي x و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) اذا كان

lim -∞

f(x) = b

( b∈IR)

فان المستقيم ذو المعادلة y=b مقارب ل (C) بجوار -∞.

2) اذا كان

lim + ∞

f(x) = b

(b∈IR)

فان المستقيم ذو المعادلة y=b مقارب ل (C) بجوار +∞.

1.3.2 مثال

لتكن f دالة عددية معرفة كما يلي

f(x) =	3x - 5
	x - 2

لتحديد المقاربات لمنحنى دالة عددية كما ذكرنا سابقا ينبغي معرفة محدات مجموعة تعريف هذه الدالة

الدالة f معرفة اذا كان x-2≠0 أي x≠2
ومنه فان D=]-∞;2[∪]2;+∞[
اذن توجد أربع محدات

- ∞

2-

2+

+ ∞

ندرس الآن الحالتين -∞ و +∞.

lim -∞	f(x) =	lim -∞	3x - 5	=	lim -∞	3x
			x - 2			x

lim -∞

f(x) = 3

اذن

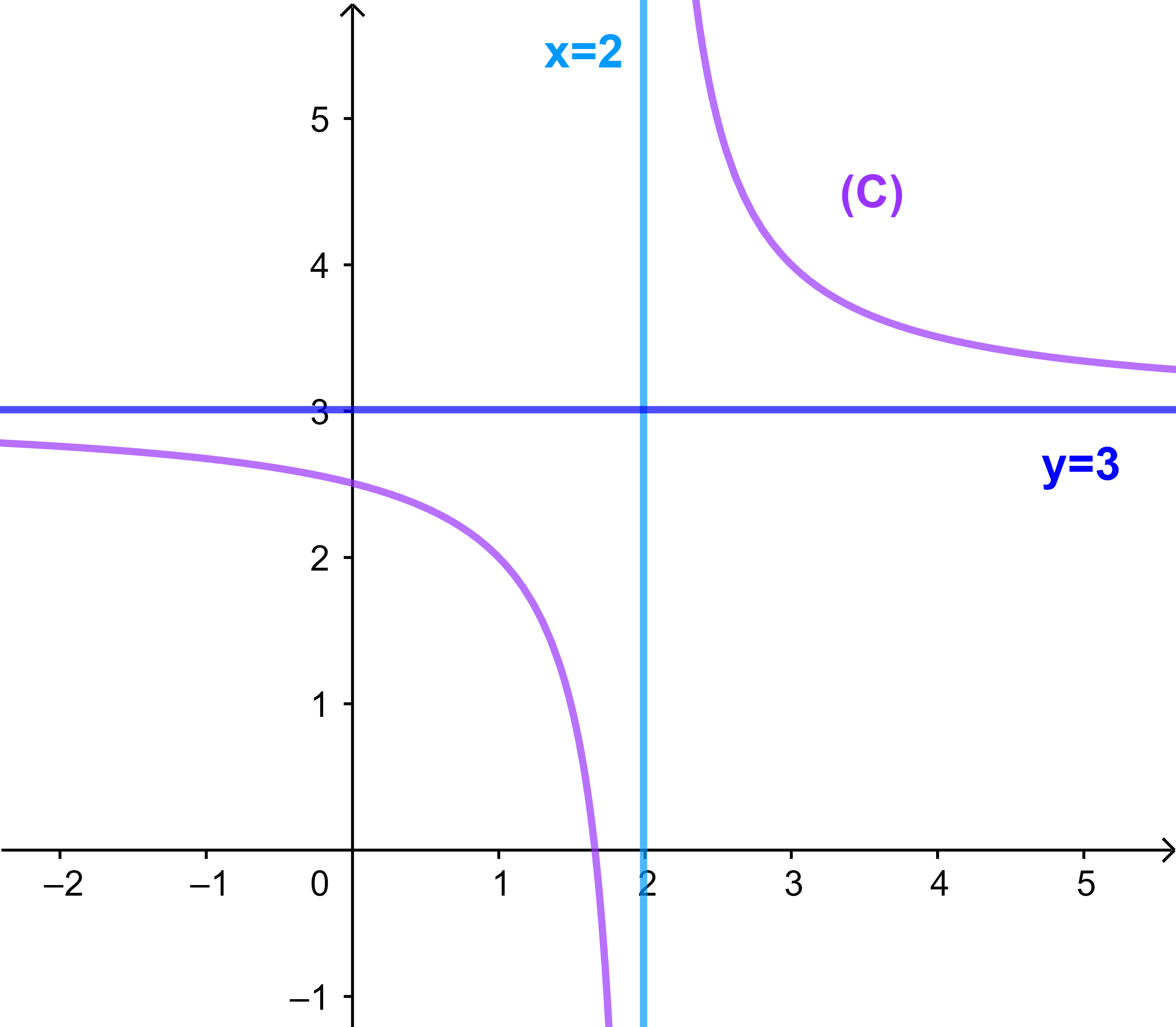
اذن المستقيم (D): y=3 مقارب (C) بجوار -∞.

lim +∞	f(x) =	lim +∞	3x - 5	=	lim +∞	3x
			x - 2			x

lim +∞

f(x) =

3 اذن

اذن المستقيم (D): y=3 مقارب (C) بجوار +∞.