1.3 Asymptote parallèle à l'axe des abscisses

1.3.1 Définitions

Soient f une fonction et (C) sa courbe dans un repère orthonormé (O;i^→;j^→) et b∈IR.
1) La droite d'équation y=b est asymptote à (C) au voisinage de -∞

si

lim -∞

f(x) = b

2) La droite d'équation y=b est asymptote à (C) au voisinage de +∞

si

lim + ∞

f(x) = b

1.3.2 Exemple

Soit f une fonction numérique définie par

f(x) =	3x - 5
	x - 2

f est définie si x-2≠0 ou encore si x≠2
donc D=]-∞;2[∪]2;+∞[.

Il y a donc quatre bornes

2-		2+
- ∞		+ ∞

On étudie les deux cas -∞ et +∞

lim -∞	f(x) =	lim -∞	3x - 5
			x - 2
	=	lim -∞	3x
			x

donc

lim -∞

f(x) = 3

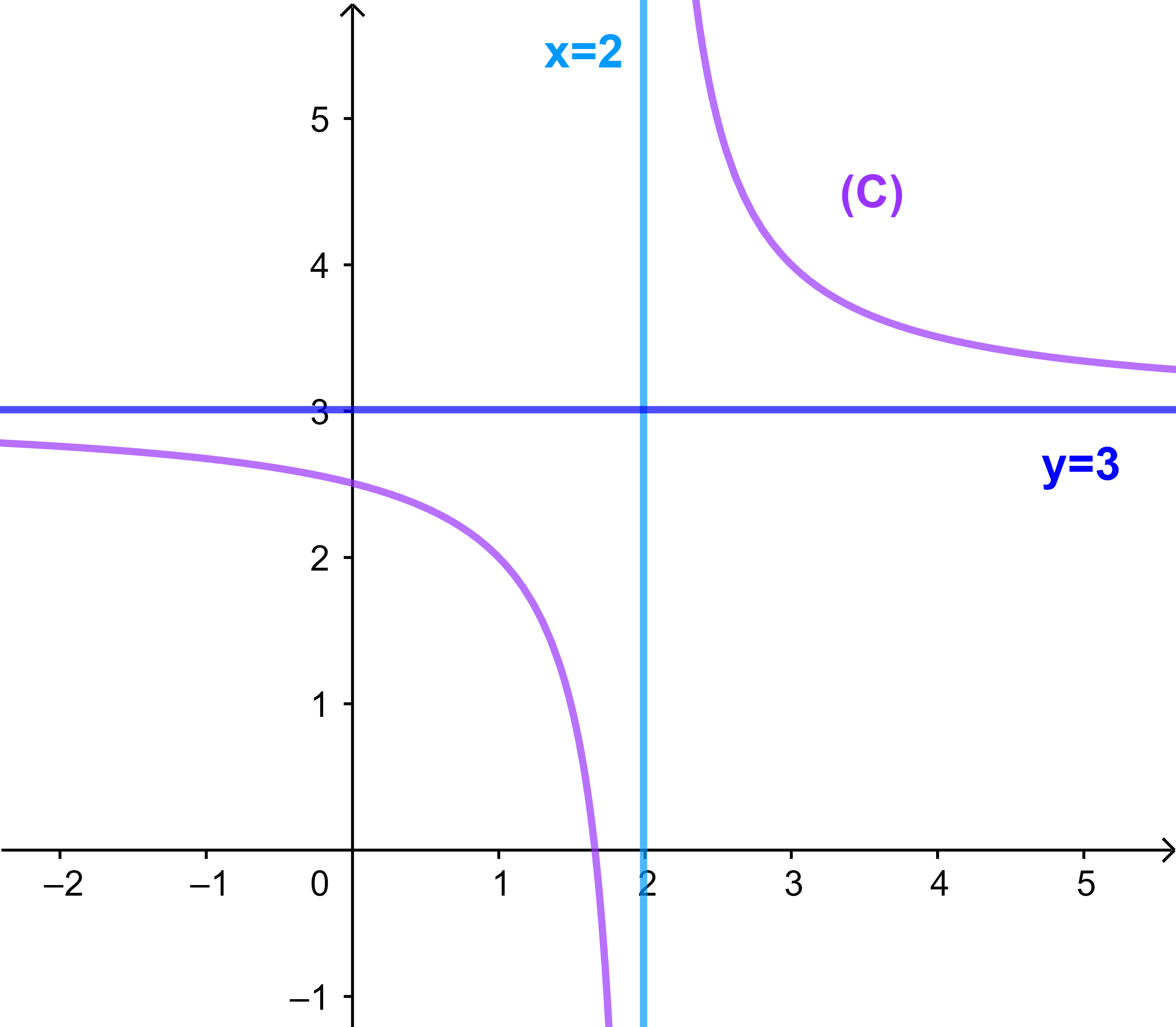
Ainsi la droite (D): y=3 est asymptote à (C) au voisinage de -∞

lim +∞	f(x) =	lim +∞	3x - 5
			x - 2
	=	lim +∞	3x
			x

donc

lim +∞

f(x) = 3

ainsi la droite (D): y=3 est asymptote à (C) au voisinage de +∞.