(5) دراسة دالة عددية
2.1.2 مثال 2
لتكن f دالة عددية ذات المتغير x معرفة كما يلي
f(x)=-x²+4x
و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i→;j→).
1) حدد D مجموعة تعريف الدالة f.
2) احسب النهايتين التاليتين
lim - ∞ |
f(x) | lim + ∞ |
f(x) |
3) احسب f'(x) حيث x∈D وادرس رتابة الدالة f وانشئ جدول تغيراتها واستنتج مطرافا لها.
4) (a) انشئ (C).
(b) حل مبيانيا المعادلة f(x)=0.
(c) حل مبيانيا المتراجحة f(x)≤0.
(d) حل مبيانيا المتراجحة
3≤f(x)≤4.
تصحيح
1) لدينا f حدودية اذن D=IR.
2) حساب النهايات.
lim - ∞ |
f(x) | = | lim - ∞ |
-x² = - ∞ |
lim + ∞ |
f(x) | = | lim + ∞ |
-x² = - ∞ |
3) f دالة حدودية اذن قابلة للاشتقاق على IR.
ليكن x∈IR
f'(x)=(-x²+4x)'=-2x+4
اذن لكل (x∈IR) f'(x)=-2x+4.
اشارة f'(x)
f'(x)=0 ⇔ -2x+4=0
⇔ -2x=-4 ⇔ 2x=4 ⇔ x=2.
f'(x) تكتب على الشكل ax+b
ولدينا a=-2<0 اذن
| x | -∞ | 1 | +∞ | |||
| -2x + 4 | + | 0 | - |
اذا كان x∈]-∞;2[ فان f'(x)>0.
اذا كان x∈]2;+∞[ فان f'(x)<0
وبالتالي الدالة f تزايدية قطعا على ]-∞;2] وتناقصية قطعا على [2;+∞[.
جدول التغيرات
| x | -∞ | 2 | +∞ | |||
| f '(x) | + | 0 | - | |||
| f | -∞ |
↗ |
4 | ↘ |
-∞ |
الدالة المشتقة f' تنعدم في 2 وتتغير اشارتها من + الى - اذن الدالة f تقبل قيمة قصوى f(2)=4.
4) (a) منحنى الدالة f
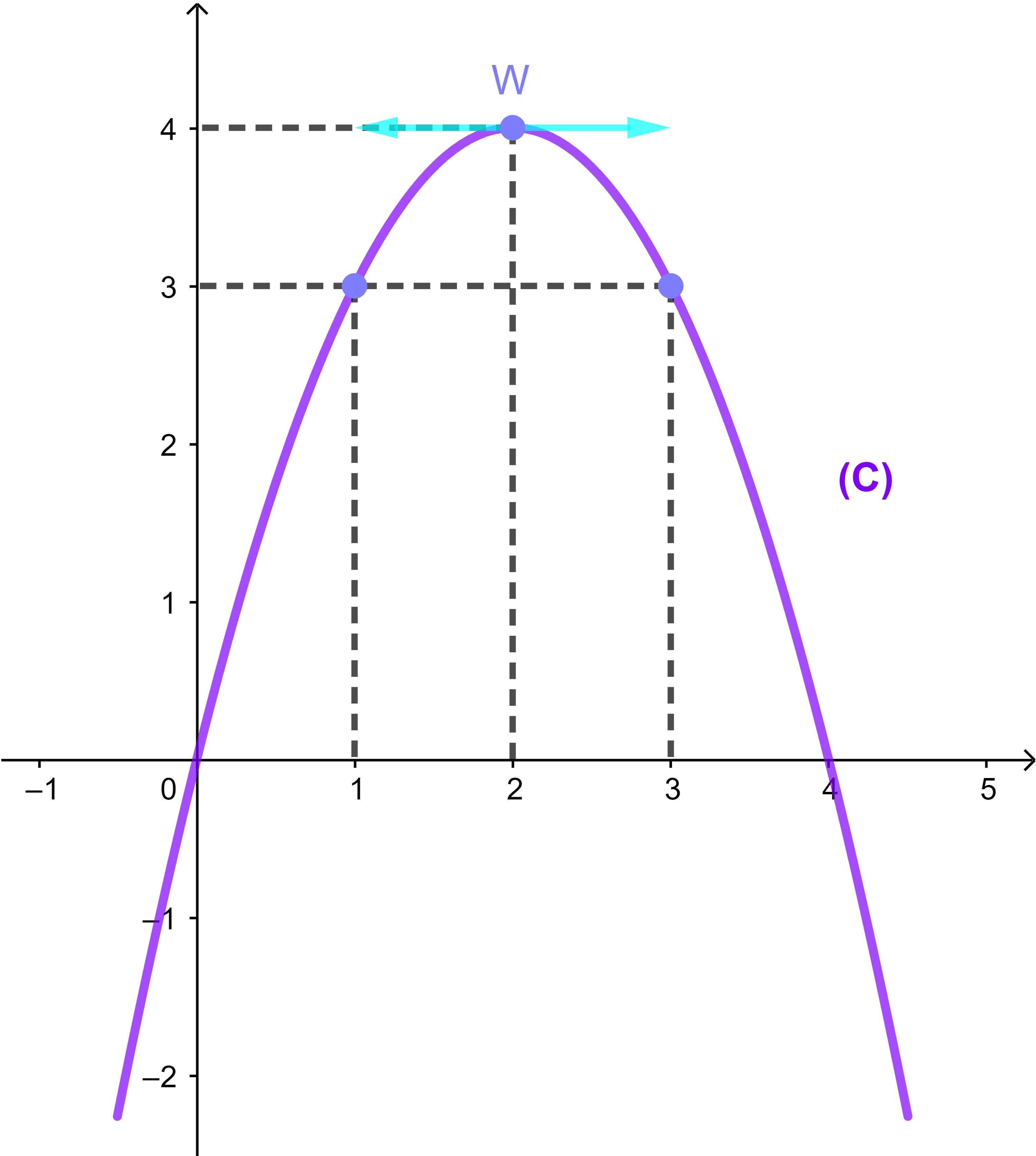
(b) حل مبيانيا المعادلة f(x)=0 يعني تحديد عدد نقط تقاطع المنحنى (C) ومحور الافاصيل (Ox).
المنحنى (C) يقطع محور الأفاصيل في نقطتين وبالتالي المعادلة f(x)=0 تقبل حلين a=0 و b=4.
(c) حلول مبيانيا المتراجحة f(x)≤0 يعني تحديد المجالات التي يكون المنحنى (C) تحت محور الافاصيل .
في المجالين ]-∞;0] و [4;+∞[ المنحنى (C) تحت محور الافاصيل (Ox) اذن مجموعة حلول المتراجحة f(x)≤0
S2=]-∞;0]∪[4;+∞[.
(d) حلول مبيانيا المتراجحات 3≤f(x)≤4
يعني تحديد المجالات التي يكون المنحنى (C) بين المستقيمين
(D): y=3 و (D'): y=4.
ملاحظة f(1)=3 و f(2)=4 و f(3)=3
اذا اسقطنا الجزء الصغير من الشلجم بين المستقيمين نجد قطعة ممثلة بالمجال [1;3]
اذن مجموعة الحلول S3=[1;3].