تمرين 1 tp

لتكن f دالة عددية و (C) المنحنى الممثل لها في معلم.

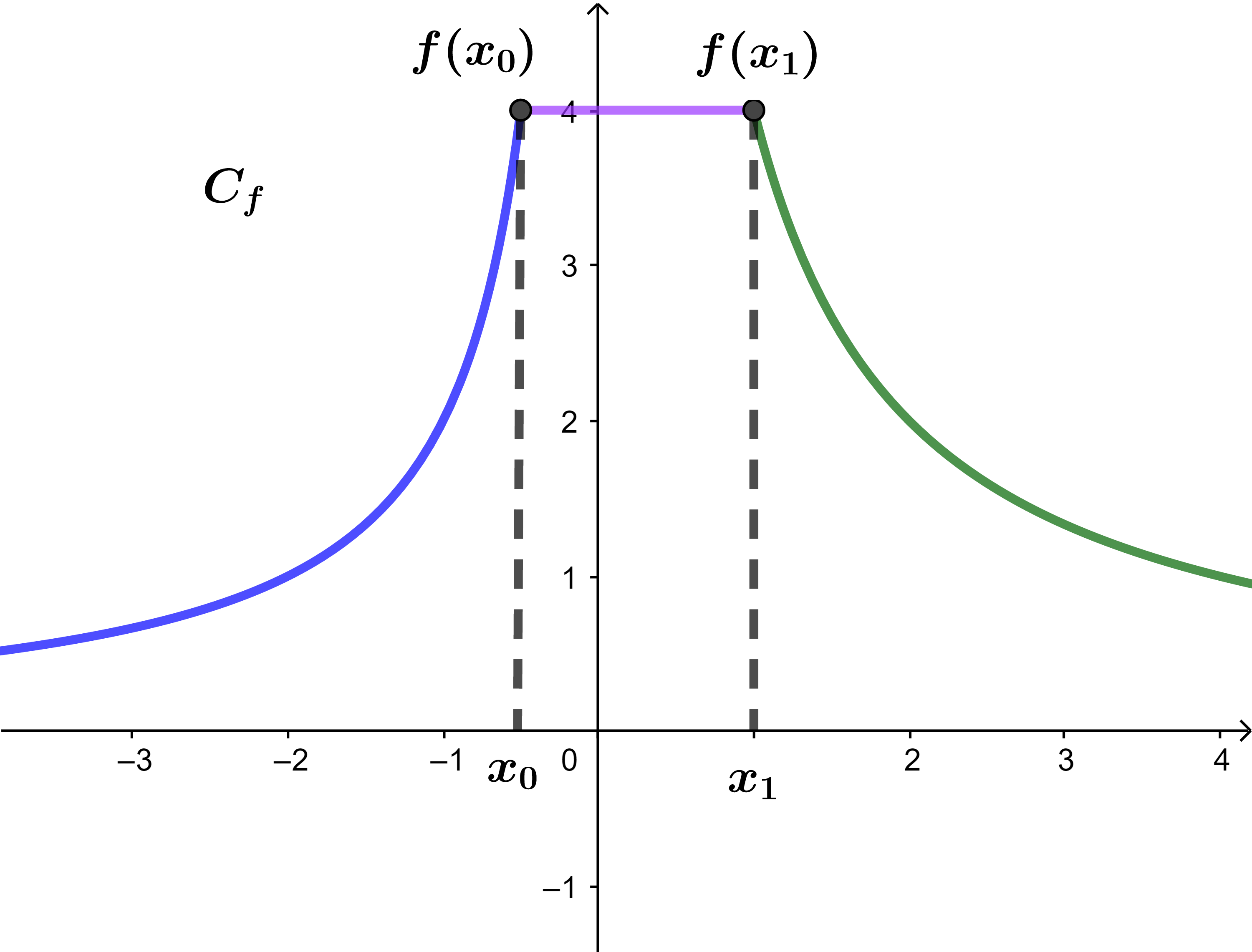
حدد مبيانيا رتابة الدالة f في كل من المجالات التالية
]-∞;x₀] و [x₀;x₁] و [x₁;+∞[.

تصحيح

1) f تزايدية قطعا على ]-∞;x₀].

2) f ثابتة على [x₀;x₁].
3) f تناقصية قطعا على [x₁;+∞[.
جدول تغيرات الدالة f.

x	-∞		x0		x1		+∞
f		↗		----		↘

4.1.5 معدل تغيرات دالة عددية

تعريف
لتكن f دالة عددية و D مجموعة تعريفها
نعتبر عنصرين مختلفين x و y من D.
معدل تغير الدالة f بين العددين x و y هو العدد الذي نرمز له ب T(x;y) ومعرف كما يلي

T(x ; y) =	f(x) - f(y)
	x - y

خاصيات 1
لتكن f دالة عددية معرفة على مجال I.
1) تكون f تزايدية على I اذا كان لكل عنصرين مختلفين x و y من I لدينا T(x;y)≥0.
2) تكون f تناقصية على I اذا كان لكل عنصرين مختلفين x و y من I لدينا T(x;y)≤0.
3) تكون f ثابتة على I اذا كان لكل عنصرين مختلفين x و y من I لدينا T(x;y)=0.

خاصيات 2
1) تكون f تزايدية قطعا على I اذا كان لكل عنصرين مختلفين x و y من I لدينا T(x;y)>0.
2) تكون f تناقصية قطعا على I اذا كان لكل عنصرين مختلفين x و y من I لدينا T(x;y)<0.

تمرين 1 tp

لتكن f دالة عددية معرفة كما يلي f(x)=x²+4x.
1) ادرس رتابة الدالة f على المجالين
I=]-∞;-2] و J=[-2;+∞[.
2) انشئ جدول تغيرات الدالة f.

تصحيح

لدراسة تغيرات دالة عددية يمكن استعمل معدل تغيراتها ليكن x و y عنصرين مختلفين من IR
f(x)-f(y)=x²+4x-(y²+4y)
=(x²-y²)+4(x-y)=(x-y)(x+y)+4(x-y)
=(x-y)(x+y+4).

اذن

T(x ; y) =	f(x) - f(y)	=	(x-y)(x+y+4)
	x - y		x - y

بعد الاختزال نحصل على T(x;y)=x+y+4.

1) ليكن x و y∈]-∞;-2] اذن x≤-2 و y≤-2
ومنه فان x+y<-4
(المتفاوتة اصبحت قطعا لان x و y مختلفان لايمكن ان يأخذان نفس القيمة - 2 في نفس الوقت )
اذن x+y+4<0
ومنه فان T(x;y)<0 وهذا يعني أن الدالة f تناقفصية قطعا على المجال I.
ليكن x و y∈[-2;+∞[ حيث x≠y
اذن x≥-2 و y≥-2 ومنه فان x+y>-4.

(المتفاوتة اصبحت قطعا لان x و y مختلفان لايمكن ان يأخذان نفس القيمة - 2 في نفس الوقت ).
اذن x+y+4>0
ومنه فان T(x;y)>0 وهذا يعني أن الدالة f تزايدية قطعا على المجال J.
2) جدول التغيرات

x		-∞		-2		+∞
f			↗	-4	↘