4.2 مطارف دالة عددية

4.2.1 القيمة الدنيا لدالة عددية

تعريف
f دالة عددية معرفة على مجال I (I⊂D), القيمة الدنيا لدالة عددية f على المجال I اصغر قيمة لصور عناصر المجال I بواسطة الدالة f
وبتعبير آخر
m قيمة دنيا ل f على I اذا وجد عدد حقيقي a في المجال I بحيث لكل x∈I لدينا f(x)≥m=f(a).

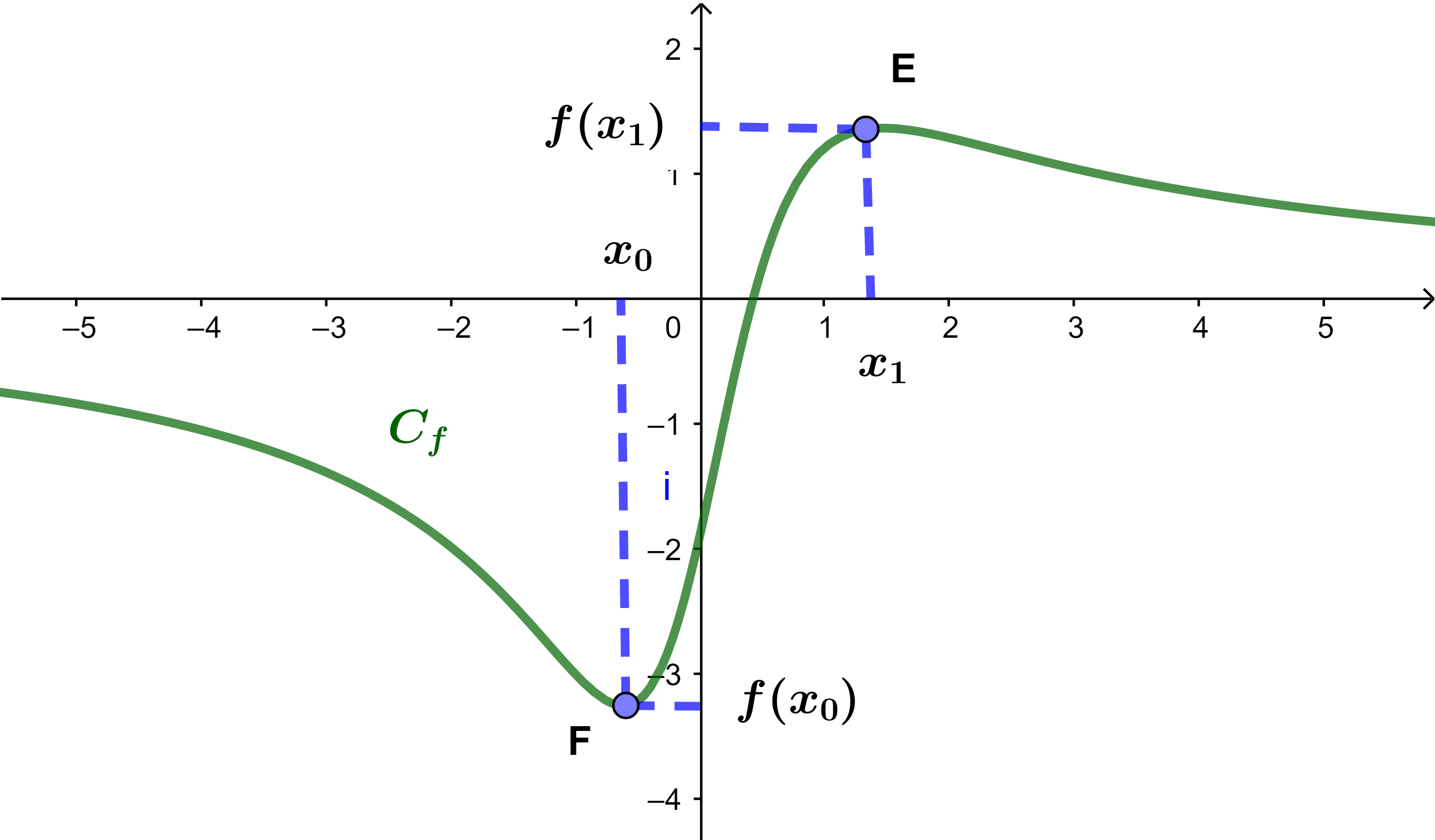
f(x₀) قيمة دنيا للدالة f عند x₀ و f(x₁) قيمة قصوى للدالة f عند x₁.

مثال
لتكن f دالة عددية لمتغير حقيقي x بحيث
f(x)=x²+1.
بين ان 1 قيمة دنيا للدالة f.

تصحيح

لكل x∈IR لدينا x²≥0 اذن x²+1≥1
ومنه فان لكل x∈IR لدينا f(x)≥1
هذه المتفاوتة غير كافية للقول أن 1 قيمة دنيا للدالة f لانه ينبغي معرفة ان كان العدد 1 صورة لعدد بواسطة الدالة f.

وبعبارة أخرى يبقى معرفة هل يوجد عنصر a من I=IR بحيث f(a)=1
لذلك يكفي حل المعادلة f(x)=1 في المجال I
f(x)=1 يعني x²+1=1 يعني x²=0 اي x=0
اذن 1=f(0) وبالتالي 1 قيمة دنيا ل f عند 0.

4.2.2 القيمة القصوى لدالة عددية

تعريف
لتكن f دالة عددية معرفة على مجال I حيث (I⊂D) القيمة القصوى لدالة عددية f على المجال I اكبر قيمة لصور عناصر المجال I بواسطة الدالة f
وبتعبير آخر
M قيمة قصوى ل f على I اذا وجد عدد حقيقي a في المجال I بحيث لكل x∈I لدينا f(x)≤M=f(a).

مثال
لتكن f دالة عددية معرفة كما يلي
f(x)=-x²+3.
بين ان 3 قيمة قصوى للدالة f.

تصحيح
لكل x∈IR لدينا - x²≤0 اذن -x²+1≤3
ومنه فان لكل x∈IR لدينا f(x)≤3
يبقى معرفة هل يوجد عنصر a من I=IR
بحيث f(a)=3 ?

نحل اذن المعادلة f(x)=3 في المجال I
f(x)=3 ⇔ -x²+3=3
⇔ x²=0 ⇔ x=0
اذن 3=f(0) وبالتالي 3 قيمة قصوى ل f عند 0.

4.2.3 مطارف دالة عددية

تعريف
لتكن f دالة عددية معرفة على مجال I و a∈I.
نقول ان f(a) مطراف للدالة f على I اذا كان قيمة قصوى او قيمة دنيا للدالة f على المجال I.