1.2.3 الدالة الفردية

لتكن f دالة عددية لمتغير حقيقي x و D مجموعة تعريفها.
نقول ان f دالة فردية اذا تحقق ما يلي
1) لكل x∈D فان -x∈D.
2) لكل x∈D فان f(-x)=-f(x).

ملاحظة
نفترض ان f دالة فردية
اذا كان x∈D فان مقابله ايضا ينتمي الى D
وبالاضافة الى ذلك لهما صورتان متقابلتان بواسطة الدالة f اي (f(-x)=-f(x)).

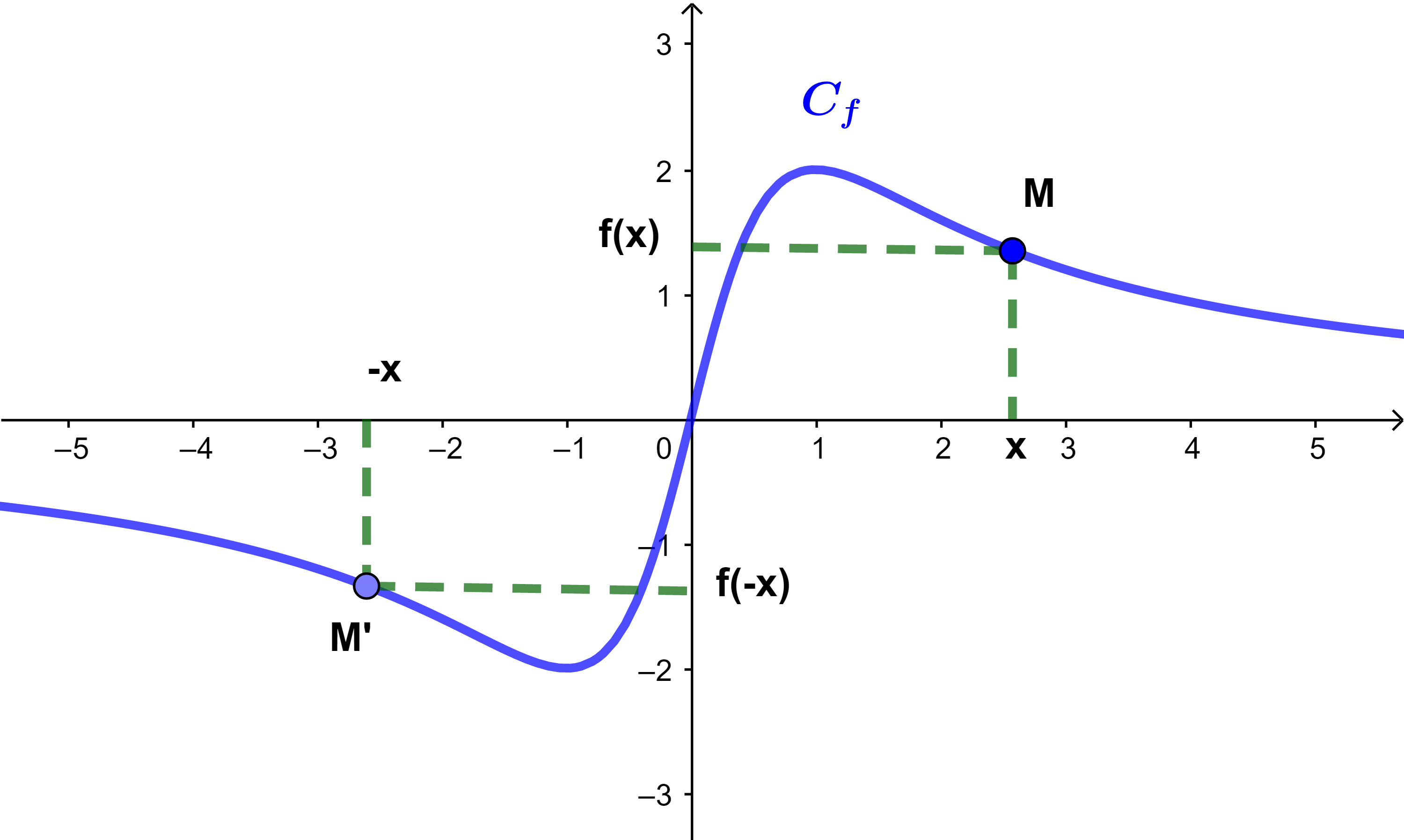
التأويل الهندسي لدالة فردية
لتكن f دالة فردية و C_f منحناها الممثل في المعلم
(O;i^→;j^→)
بما ان لكل x∈IR لدينا f(-x)=-f(x)
فان النقطتين M(x;f(x)) و M'(-x;-f(x)) متماثلتان بالنسبة لاصل المعلم.

نتيجة منحنى دالة فردية مماثل بالنسبة لاصل المعلم.

مثال
لتكن f دالة عددية لمتغير حقيقي x بحيث f(x)=x³.
بين أن f دالة فردية.

تصحيح
(a) لكل x∈IR لدينا x³∈IR
اذن D_f=IR.
(b) بما ان D_f=IR و IR مجموعة مماثلة بالنسبة للصفر اذن لكل x∈D_f فان -x∈D_f.
(c) نقارن f(x) و f(-x).
ليكن x∈IR لدينا f(-x)=(-x)³=-x³
اذن f(-x)=-f(x)
وهذا يعني أن f دالة فردية .