3- مقارنة دالتين واشارة دالة عددية

3.1 مقارنة دالتين

3.1.1 مثال 1

ليكن x∈IR.
لدينا 3≥1 اذن x+3>x+1.
نعتبر الدالتين العدديتين f و g بحيث
f(x)=x+3 و g(x)=x+1.
لدينا اذن (∀x∈IR)(f(x)>g(x))
ونكتب f>g.
ننشئ في نفس المعلم المنحنيين (C_f) و (C_g) للدالتين f و g.

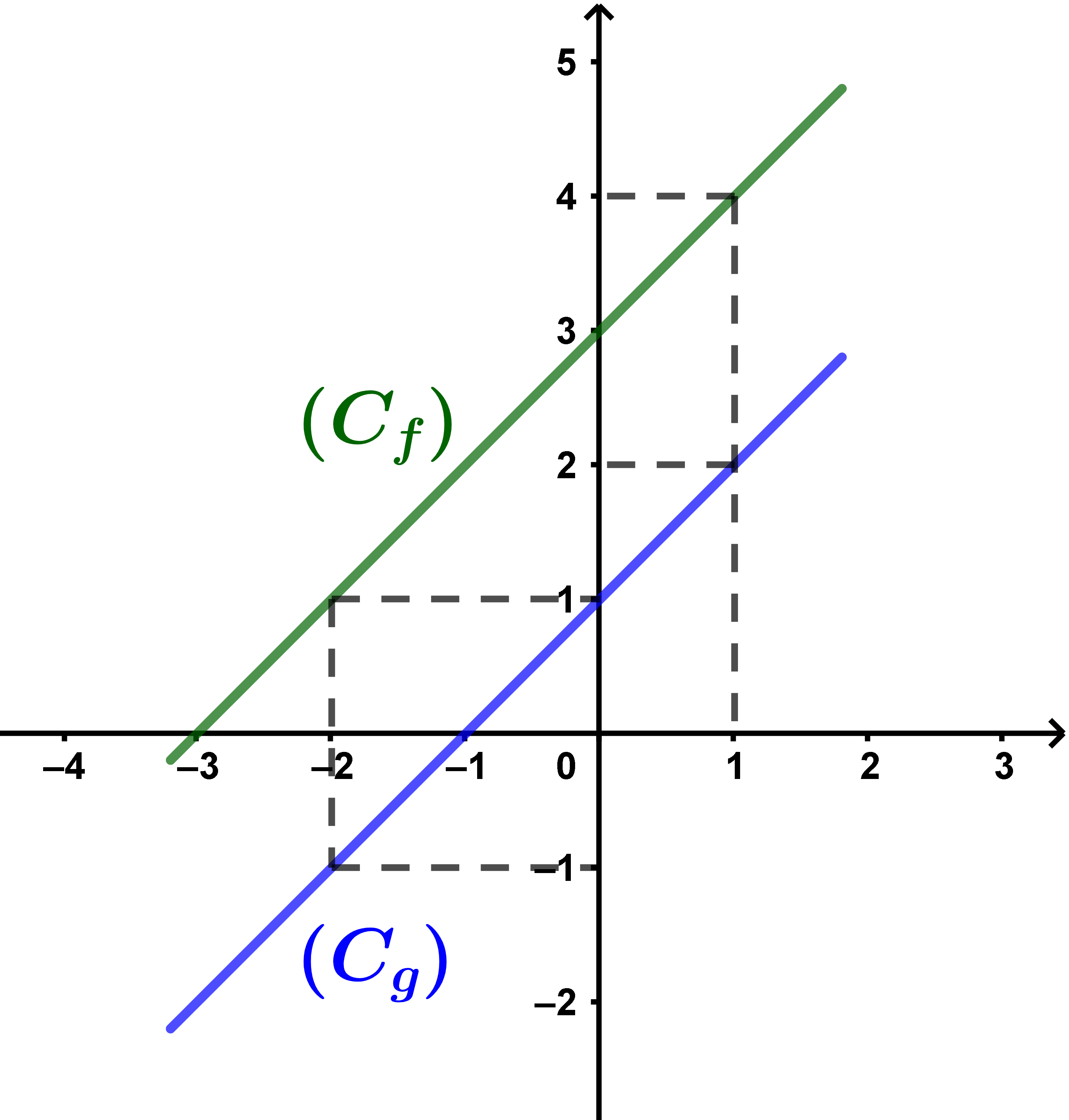
منحنى الدالة f فوق منحنى الدالة g وهذا يعني أن f>g.

3.1.1 2 مثال

لتكن f و g دالتين عدديتين معرفتين كما يلي
f(x)=x²-2x+2 و g(x)=x².
قارن جبريا وهندسيا g و f.

تصحيح
مقارنة f و g جبريا.
ندرس اذن اشارة العدد f(x)-g(x).
(a) f(x)-g(x)=0 ⇔ x²-2x+2-x²=0
⇔ -2x+2=0 ⇔ x=1.

(b) f(x)-g(x)>0 ⇔ -2x+2>0
⇔ -2x>-2 ⇔ 2x<2 ⇔ x<1
ومنه فان f>g ⇔ x∈]-∞;1[.
(c) f(x)-g(x)<0 ⇔ -2x+2<0
⇔ -2x<-2 ⇔ 2x>2 ⇔ x>1
ومنه فان f<g ⇔ x∈]1;+∞[.

2) التمثيل المبياني للدالتين

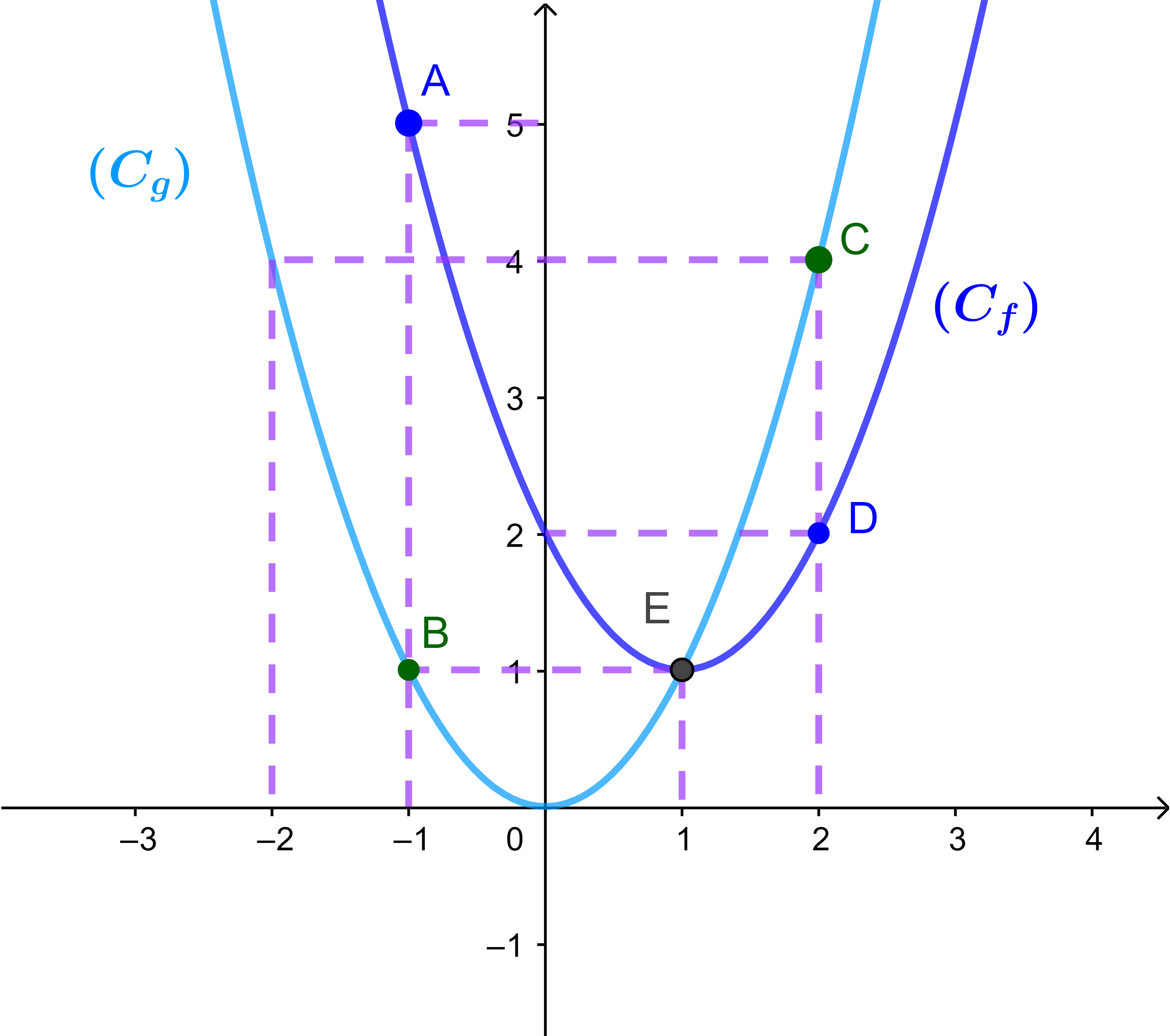
منحنيا الدالتين يلتقيان في نقطة واحدة
E(1;1) وهذا يعني ان الدالتين متساويتان اذا كان x=1.
(C_f) فوق (C_g) في المجال ]-∞;1]
وهذا يعني أن f ≥ g
(C_f) تحت (C_g) في المجال [1;+∞[
وهذا يعني أن f≤g.

3.1.3 تعريف 1

لتكن f و g دالتين عدديتين و D_f و D_g مجموعتي تعريفهما على التوالي.
g و f متساويتان اذا تحققت الشروط التالية
1) D_f=D_g
2) (∀x∈D): f(x)=g(x).

3.1.4 تعريف 2

لتكن f و g دالتين عدديتين و معرفتين على مجال I.
1) f < g اذا كان (∀x∈I): f(x) < g(x)
ونقول هندسيا أن منحنى الدالة f تحت منحنى الدالة g.
2) f > g اذا كان (∀x∈I): f(x) > g(x)
ونقول هندسيا أن منحنى الدالة f فوق منحنى الدالة g.