3- Comparaison de deux fonctions et signe d'une fonction

3.1 Comparaison de deux fonctions

3.1.1 Exemple 1

Soit x∈IR. On a 3>1 donc x+3>x+1
On considère deux fonctions f et g définies par
f(x)=x+3 et g(x)=x+1
On a donc (∀x∈IR)(f(x)>g(x))
et on écrit f>g.

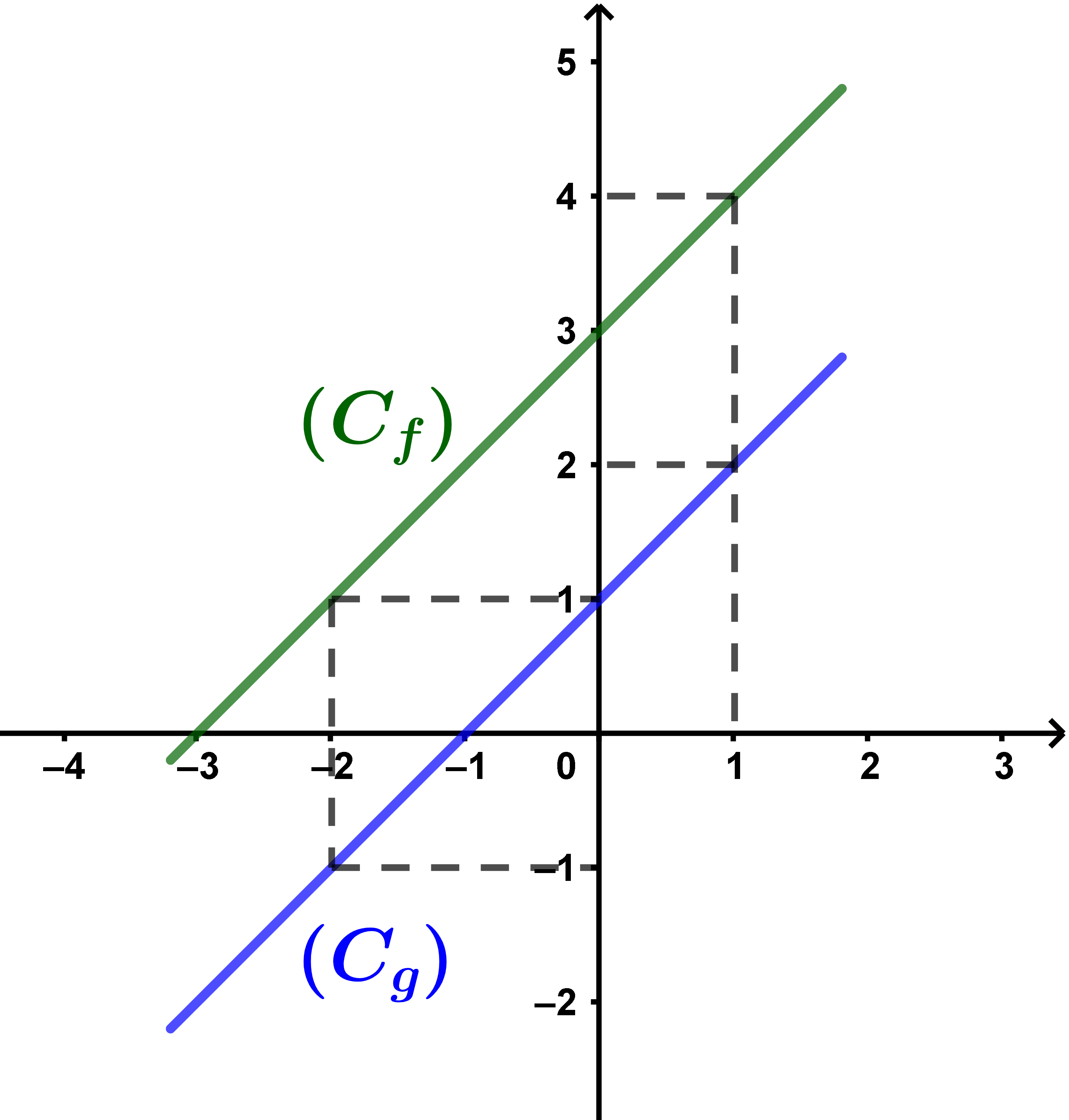
Les courbes (C_f) et (C_g) de f et g sont représentées dans un même repère.

(C_f) est au dessus de (C_g) signife donc f>g.

3.1.2 Exemple 2

Soient f et g deux fonctions définies par
f(x)=x²-2x+2 et g(x)=x²
Comparons graphiquement et algébriquement f et g.

1) Comparaisons algébrique.
On étudie le signe de f(x)-g(x).
f(x)-g(x)=x²-2x+2-x²=-2x+2
(a) f(x)-g(x)=0 ⇔ -2x+2=0 ⇔ x=1
donc f=g si x=1.

(b) f(x)-g(x)>0 ⇔ -2x+2>0 ⇔ -2x>-2
⇔ 2x<2 ⇔ x<1
donc f>g sur ]-∞;1[.
(c) f(x)-g(x)<0 ⇔-2x+2<0 ⇔ -2x<-2.
⇔ 2x>2 ⇔ x>1
donc f<g sur ]1;+∞[.

2) Comparaisons graphique

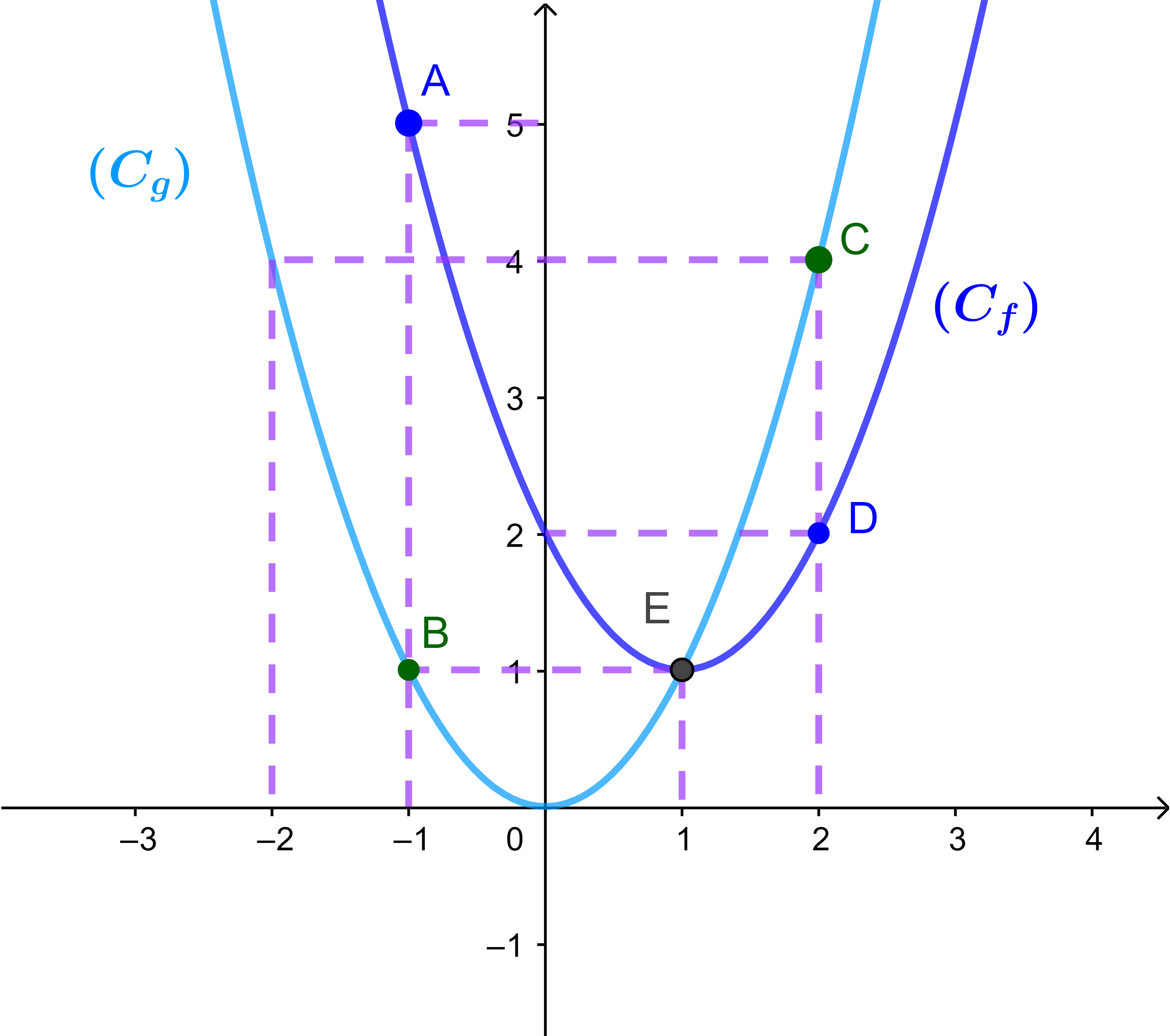
Les courbes de f et g se coupent en un seul point E(1,1)
donc f=g si x=1.
Si x∈]-∞;1] alors la courbe (C_f) est au-dessus de (C_g)
donc f>g sur ]-∞;1[.
Si x∈]1;+∞[ alors la courbe (C_f) est au-dessous de (C_g)
donc f<g sur ]1;+∞[.

3.1.3 Définition 1

Soient f et g deux fonctions numériques et D_f et D_g réspéctivement leurs ensembles de définitions.
f et g sont égales et on écrit f=g si les deux conditions suivantes sont vérifiées
1) D_f=D_g.
2) (∀x∈D): f(x)=g(x).

3.1.4 Définition 2

Soient f et g deux fonctions numériques définies sur un intervalle I.
1) f<g si (∀x∈I): f(x)<g(x)
et on dit graphiquement que (C_f) est au-dessous de (C_g) sur I.
2) f>g si (∀x∈I): f(x)>g(x)
et on dit graphiquement que (C_f) est au-dessus de (C_g) sur I.