4- تغيرات دالة عددية ومطارف دالة

4.1 تغيرات دالة عددية

4.1.1 انشطة

امتلأ خزان ماء في مدة دقيقتين ونصف بمقدار 2م³/د .
1) (a) حدد الدالة التي تربط بين المدة الزمنية من 0 الى 2,5 وكمية الماء في الخزان الموافقة لها.
(b) حدد كمية الماء الموجودة في الخزان عند الدقيقة 2,5.
(c) حدد كمية الماء في الخزان عند الدقيقية 1 ثم عند الدقيقة 2.

2) نفترض ان الخزان يفرغ مياهه بنفس المدة وبنفس المقدار أي متيرين في الدقيقة.
(a) حدد الدالة التي تربط بين المدة الزمنية من 0 الى 2,5 وكمية الماء في الخزان الموافقة لها.
(b) حدد كمية الماء الموجودة في الخزان عند الدقيقة 1.
(c) حدد كمية الماء في الخزان عند الدقيقة 2.

تصحيح

1) عند الدقيقة الاولى تكون كمية الماء في الخزان مترين مكعب وفي الدقيقة 2 تنضاف متران الى الخزان وتصبح الكمية 2.2=4 امتار وفي الدقيقة x تكون كمية الماء في الخزان 2x اذن الدالة r التي تربط المدة الزمنية x∈[2,5;0] وكمية الماء الموجودة في الخزان معرفة كما يلي
r(x)=2x.

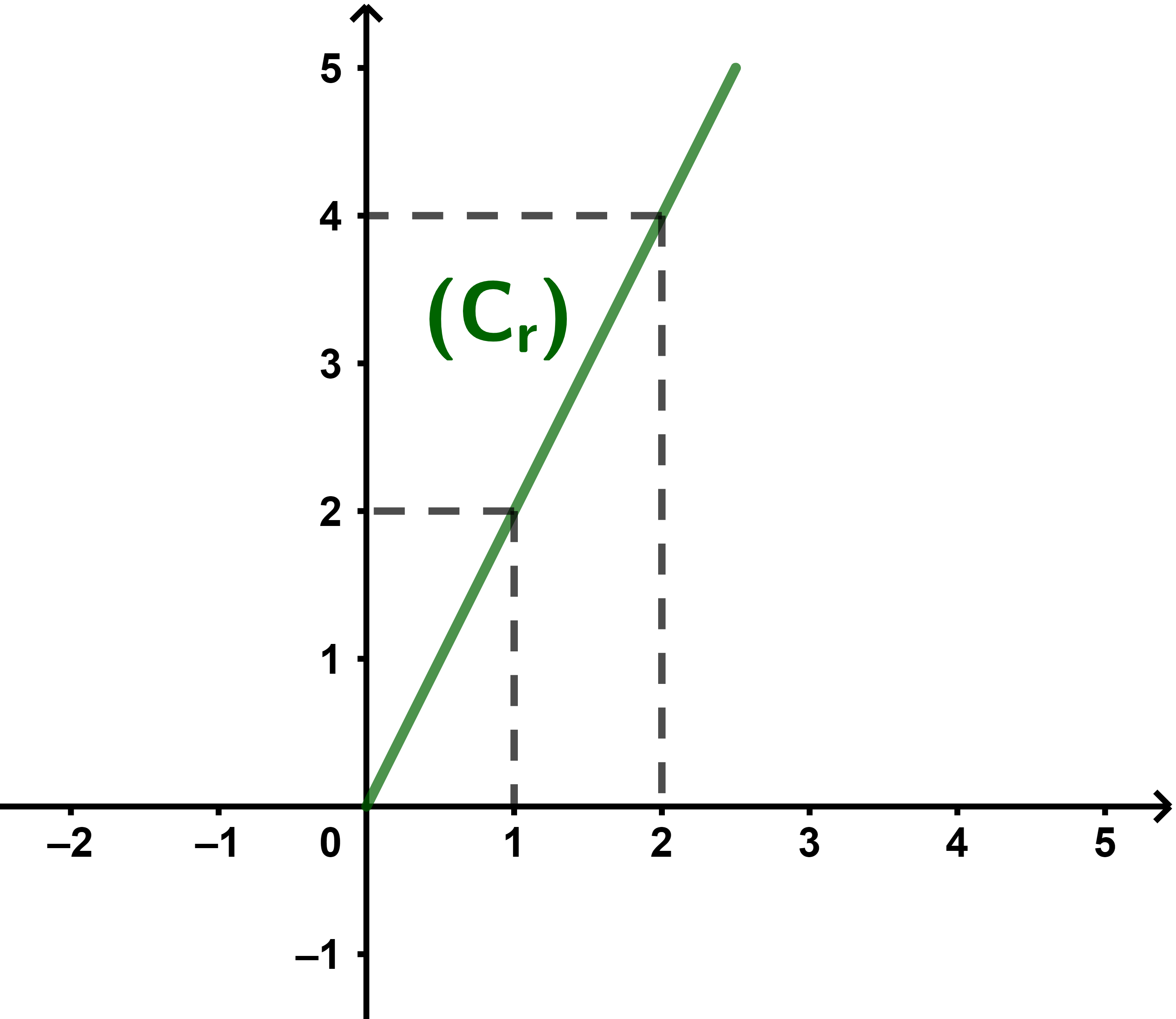
بالتعريف نقول ان الدالة r تزايدية على المجال [0;2,5].

2) عند الدقيقة 0 تكون كمية الماء في الخزان 5 امتار مكعب وبعد مرور دقيقة واحدة بالضبط ينقص متران مكعب من الماء من الخزان اي يكون في الخزان 5-2=3 امتار مكعب من الماء
وفي الدقيقة 2 ينقص متران مكعب من الماء من الخزان وتصبح الكمية 5-2.2=1 متر مكعب من الماء
وفي الدقيقة x تكون كمية الماء في الخزان 5-2x اذن الدالة v التي تربط المدة الزمنية x∈[0;2,5] وكمية الماء الموجودة في الخزان معرفة كما يلي
v(x)=5-2x.

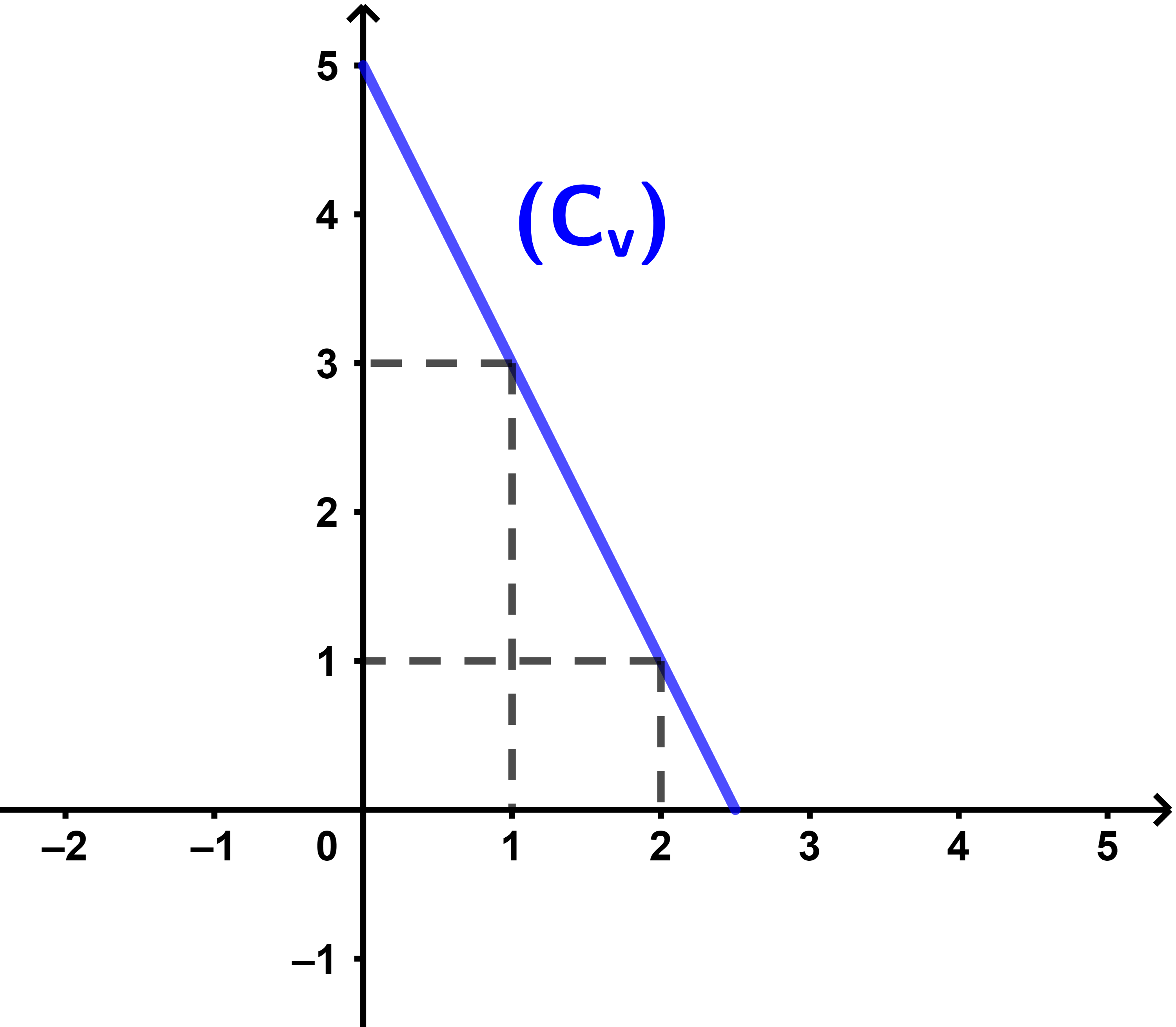
بالتعريف نقول ان الدالة v تناقصية على المجال [0;2,5].

4.1.2 الدالة التزايدية

تعاريف
لتكن f دالة عددية لمتغير حقيقي x و I مجالا ضمن D_f.
1) نقول ان f دالة تزايدية على المجال I اذا كان لكل x و y من I حيث x<y فان f(x)≤f(y).
2) نقول ان f دالة تزايدية قطعا على I
اذاكان لكل x و y من I حيث x<y فان f(x)<f(y).

4.1.3 الدالة التناقصية

تعاريف
لتكن f دالة عددية لمتغير حقيقي x و I مجالا ضمن D_f.
1) نقول ان f دالة تناقصية على المجال I اذا كان لكل x و y من I حيث x<y فان f(x)≥f(y).
2) نقول ان f دالة تناقصية قطعا على I
اذاكان لكل x و y من I حيث x<y فان f(x)>f(y).