للتذكير f دالة عددية معرفة على مجال I
القيمة الدنيا لدالة عددية f على المجال I اصغر قيمة لصور عناصر المجال I بواسطة الدالة f
وبتعبير آخر
m قيمة دنيا ل f على I اذا وجد عدد حقيقي a في المجال I بحيث لكل x∈I لدينا f(x) ≥ m = f(a)
القيمة القصوى لدالة عددية f على المجال I اكبر قيمة لصور عناصر المجال I بواسطة الدالة f
وبتعبير آخر
M قيمة قصوى ل f على I اذا وجد عدد حقيقي a في المجال I بحيث لكل x∈I لدينا f(x) ≤ M = f(a)
كل يمة قصوى أو قيمة دنيا تسمى مطرافا للدالة f على مجال I

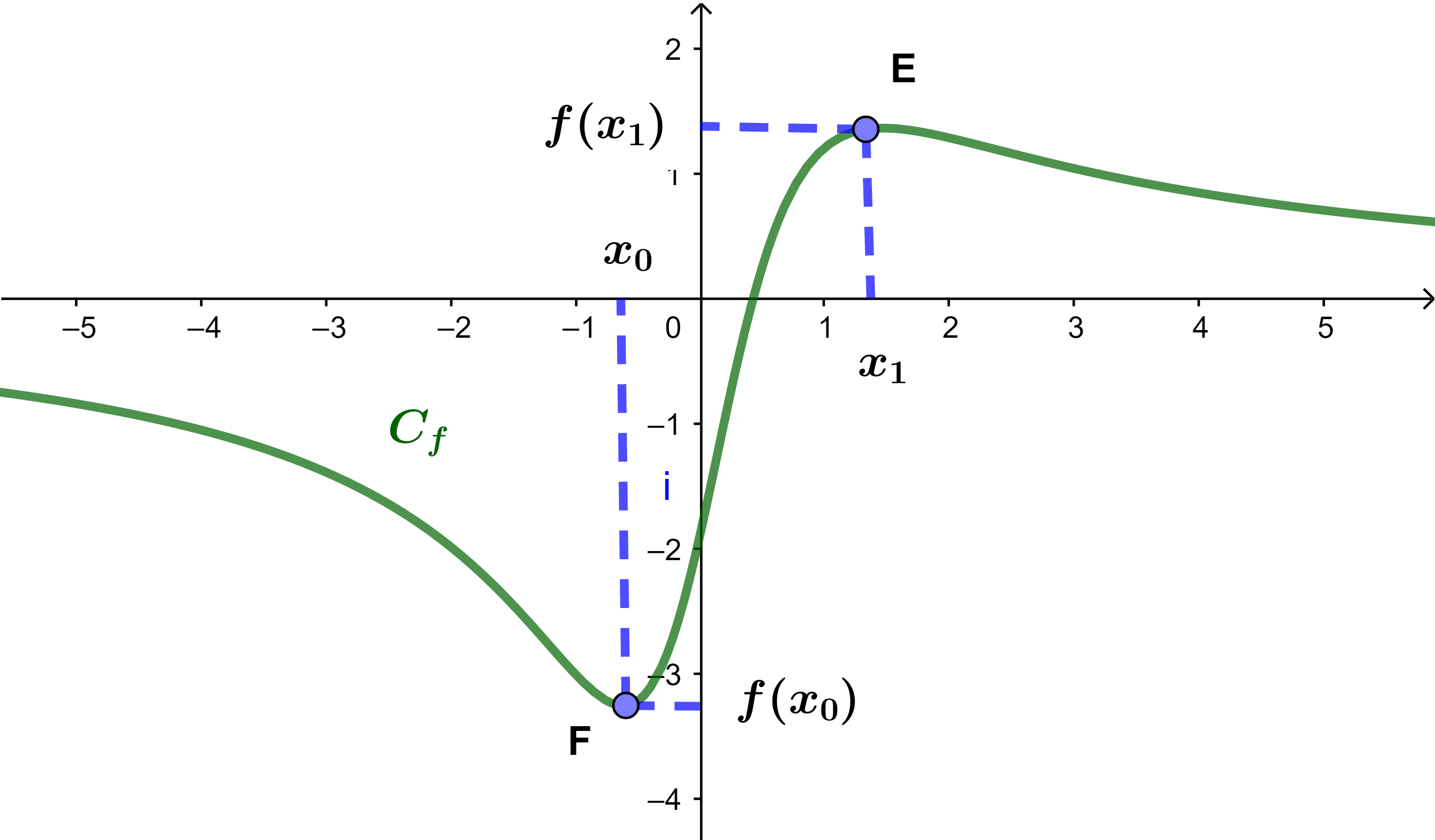
f(x₀) قيمة دنيا للدالة f عند x₀ و f(x₁) قيمة قصوى للدالة f عند x₁

تمرين 1 tp

لتكن f دالة عددية لمتغير حقيقي x بحيث
f(x) = x² + 1
بين ان 1 قيمة دنيا للدالة f

تصحيح

لكل x∈IR لدينا x² ≥ 0 اذن x²+1 ≥ 1
ومنه فان لكل x∈IR لدينا f(x) ≥ 1
هذه المتفاوتة غير كافية للقول أن 1 قيمة دنيا للدالة f ينبغي معرفة ان كان العدد 1 صورة لعدد بواسطة الدالة f
وبعبارة أخرى يجب معرفة هل يوجد عنصر a من I = IR بحيث f(a) = 1
لذلك يكفي حل المعادلة f(x) = 1 في المجال I
f(x) = 1 يعني x²+1 = 1 يعني x²=0 اي x=0
اذن 1 = f(0) وبالتالي 1 قيمة دنيا ل f عند 0

تمرين 2 tp

لتكن f دالة عددية معرفة كما يلي
f(x) = -x²+3
بين ان 3 قيمة قصوى للدالة f

تصحيح

لكل x∈IR لدينا - x² ≤ 0 اذن -x²+1 ≤ 3
ومنه فان لكل x∈IR لدينا f(x) ≤ 3
يبقى معرفة هل يوجد عنصر a من I = IR
بحيث f(a) = 3 ?
لذلك يكفي حل المعادلة f(x) = 3 في المجال I
f(x) = 3 يعني -x² + 3 = 3 يعني x² = 0
اي x=0 اذن 3 = f(0)
وبالتالي 3 قيمة قصوى ل f عند 0

تمرين 3 tp

لتكن f دالة عددية بحيث f(x) = 2x² + 4x + 5
بين ان 3 مطراف للدالة f على IR

تصحيح

لكل x∈IR لدينا f(x) - 3 = 2 x² + 4x + 5 - 3
= 2x² + 4x + 2 = 2(x²+2x+1)
= 2(x+1)² ≥ 0
اذن لكل x∈IR لدينا f(x) ≥ 3

الآن يجب معرفة هل يوجد عنصر a من المجال I بحيث f(a) = 3 ?
f(a) = 3 يعني f(a) - 3 = 0
اي 2(a+1)² = 0 اي a = -1

اذن 3 = f(-1) ومنه فان 3 قيمة دنوية للدالة f عند -1
وبالتالي 3 مطراف للدالة للدالة f عند -1

للتذكير لتكن f دالة عددية معرفة على مجال
I = [a ; b] و c∈I
1) اذا كانت f تزايدية قطعا على المجال [a ; c] وتناقصية قطعا على المجال [c ; b] فان f(c) هي قيمة قصوى للدالة f على I
2) اذا كانت f تناقصية على المجال [a ; c] وتزايدية على المجال [c;b] فان f(c) هي قيمة دنيا ل f على I

تمرين 4 tp

لتكن f دالة عددية والجدول أسفله جدول تغيراتها على المجال [0 ; 3]

x		0		1		3
f			↗	4	↘

حدد رتابة الدالة f واستنتج مطرافا لها

تصحيح

f تزايدية قطعا على [0 ; 1] وتناقصية قطعا على [1 ; 3] وبما ان f(1) = 4 فان 4 قيمة قصوى للدالة f عند 1

تمرين 5 tp

لتكن f دالة عددية والجدول أسفله جدول تغيراتها عل IR

x		-∞		-2		+∞
f			↘	3	↗

حدد رتابة الدالة f واستنتج مطرافا لها

تصحيح

f تناقصية قطعا على المجال ]-∞ ; -2]
وتزايدية قطعا على المجال [2 ; +∞[
وبما ان f(-2) = 3 فان 3 قيمة دنيا للدالة f عند -2