Rappel
Soit f une fonction numérique définie sur un intervalle I
1) La plus petite valeur des images des nombres de I par f est appelée valeur minimale de f sur I En d'autre terme
m est une valeur minimale de f sur I s'il existe un élément a dans I
tel que (∀x∈I): f(x) ≥ m = f(a).

2) La plus grande valeur des images des nombres de I par f est appelée valeur maximale de f sur I

En d'autre terme: M est une valeur maximale de f sur I s'il existe un élément a dans I
tel que (∀x∈I): f(x) ≤ M = f(a)
3) Toute valeur minimale ou maximale d'une fonction f est appelée exremum

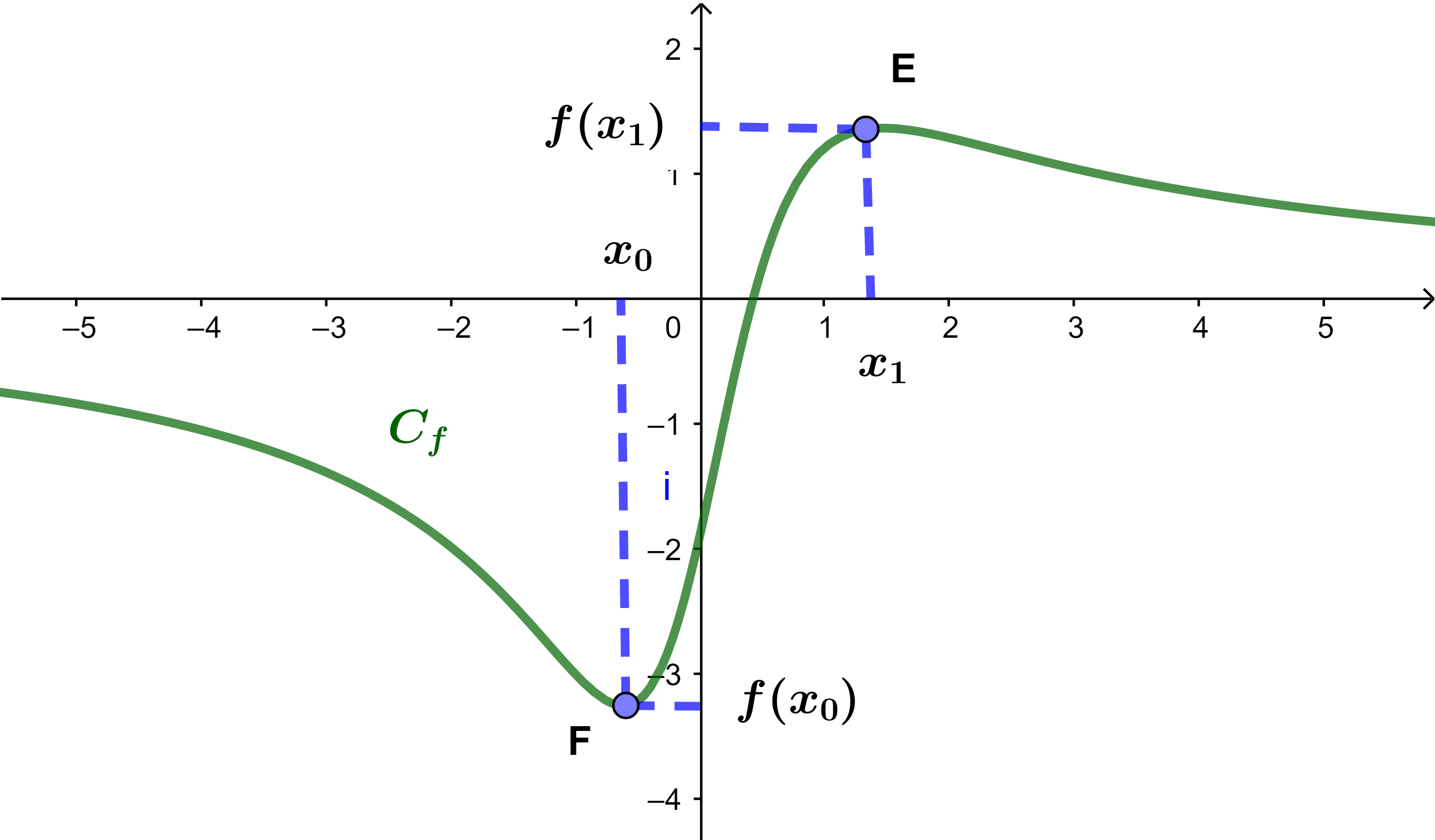
f(x₀) et f(x₁) sont deux extremums de f

Exercice 1 tp

Soit f une fonction définie par f(x) = x² + 1
Montrer que 1 est un minimum de f

Correction

On a pour tout x∈IR, x²≥0 donc x²+1≥1
ainsi pour tout x∈IR, f(x)≥1
il reste à savoir s'il existe un élément a dans I=IR tel que f(a)=1
On résout l'équation f(x)=1 dans I
f(x)=1 ⇔ x²+1=1 ⇔ x²=0 ⇔ x=0
Et donc 1=f(0) est un minimum de f

Exercice 2 tp

Soit f une fonction définie par
f(x) = -x² + 3
Montrer que 3 est un maximum de f

Correction

Pour tout (x∈IR) on a -x²≤0 donc -x²+3≤3
ainsi pour tout (x∈IR): f(x)≤3
il reste à savoir s'il existe un élément a dans I=IR tel que f(a)= 3
On résout l'équation f(x)=3 dans I
f(x)=3 ⇔ -x²+⇔ -x²=0 ⇔ x=0
ainsi 3=f(0) est un maximum de f

Exercice 3 tp

Soit f une fonction définie par
f(x) = 2x² + 4x + 5
Montrer que 3 est un extremum de f sur IR

Correction

Soit x∈IR
f(x)-3 = 2x²+4x+5-3=2x²+4x+2
= 2(x²+2x+1) = 2(x+1)²
2(x+1)² est positif donc pour tout (x∈IR): f(x)≥3
Il faut savoir s'il existe un élément a dans I tel que f(a)=3

f(a)=3 ⇔ f(a)-3=0 ⇔ 2(a+1)²=0 ⇔ a=-1
donc 3=f(-1) est bien un minimum de f
d'ou 3 est un extremum de f

Rappel
Soient f une fonction numérique définie sur un intervalle I=[a;b] et c∈I
1) Si f est croissante sur [a;c] et décroissante sur [c;b] alors f(c) est un maximum de f sur I
2) Si f est décroissante sur [a;c] et croissante sur [c;b] alors f(c) est un minimum de f sur I

Exercice 4 tp

Soit f une fonction numérique et le tableau ci-dessous son tableau de variations sur [0 ; 3]
Déterminer la monotonie de f et déduire son extremum

x		0		1		3
f			↗	4	↘

Correction

f est strictement croissante sur [0 ; 1]
et strictement décroissante sur [1 ; 3]
Donc f(1)=4 est une valeur maximale de f

Exercice 5 tp

Soit f une fonction numérique et le tableau ci-dessous son tableau de variations sur IR
Déterminer la monotonie de f et déduire son extremum

x		-∞		-2		+∞
f			↘	3	↗

Correction

f est strictement décroissante sur ]-∞;-2]
et strictement croissante sur [2;+∞[
donc f(-2)=3 est une valeur minimale de f.