للتذكير لتكن f و g دالتين عدديتين و معرفتين على مجال I
1) f < g اذا كان (∀x∈I): f(x) < g(x)
ونقول هندسيا أن منحنى الدالة f تحت منحنى الدالة g
2) f > g اذا كان (∀x∈I): f(x) > g(x)
ونقول هندسيا أن منحنى الدالة f فوق منحنى الدالة g.

تمرين 1 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) , لتكن f و g دالتين معرفتين كما يلي
f(x) = x + 3 و g(x) = x + 1
انشئ في نفس المعلم المنحنيين (C_f) و (C_g) واستنتج الوضع النسبي لهما.

تصحيح

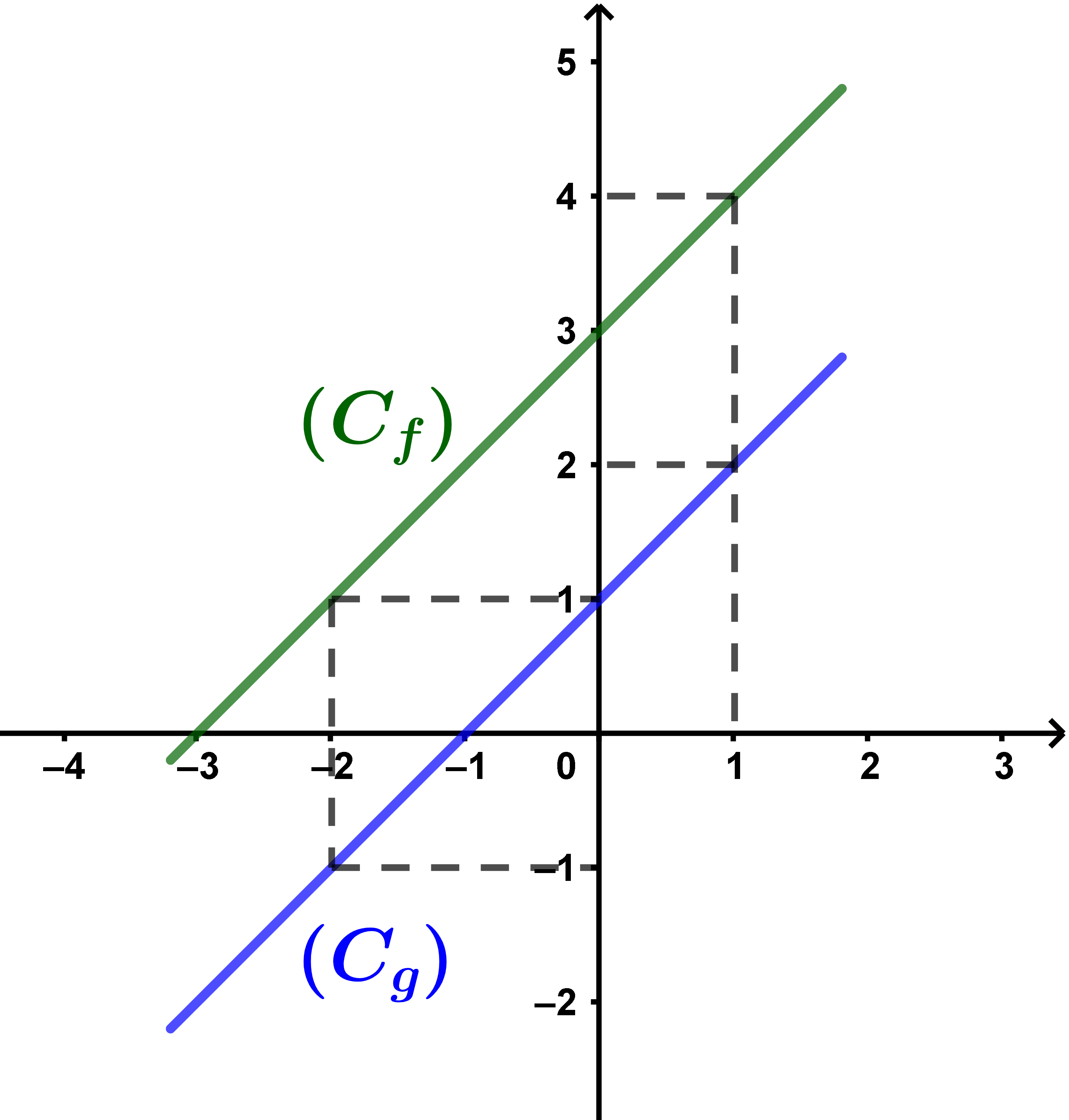
منحنى الدالة f فوق منحنى الدالة g وهذا يعني أن f > g

تمرين 2 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) , لتكن f و g دالتين معرفتين كما يلي
f(x)= x² - 2x + 2 و g(x) = x²
قارن جبريا وهندسيا g و f

تصحيح

مقارنة f و g جبريا
ندرس اذن اشارة العدد f(x) - g(x)
(a) f(x) - g(x) = 0 ⇔ x²-2x+2-x² = 0
⇔ -2x+2 = 0 ⇔ x = 1
(b) f(x) - g(x) > 0 ⇔ -2x+2 > 0
⇔ -2x > -2 ⇔ 2x < 2 ⇔ x < 1
ومنه فان f > g ⇔ x∈]-∞;1[

(c) f(x) - g(x) < 0 ⇔ -2x+2 < 0
⇔ -2x < -2 ⇔ 2x > 2 ⇔ x > 1
ومنه فان f < g ⇔ x∈]1 ; +∞[
2) التمثيل المبياني للدالتين

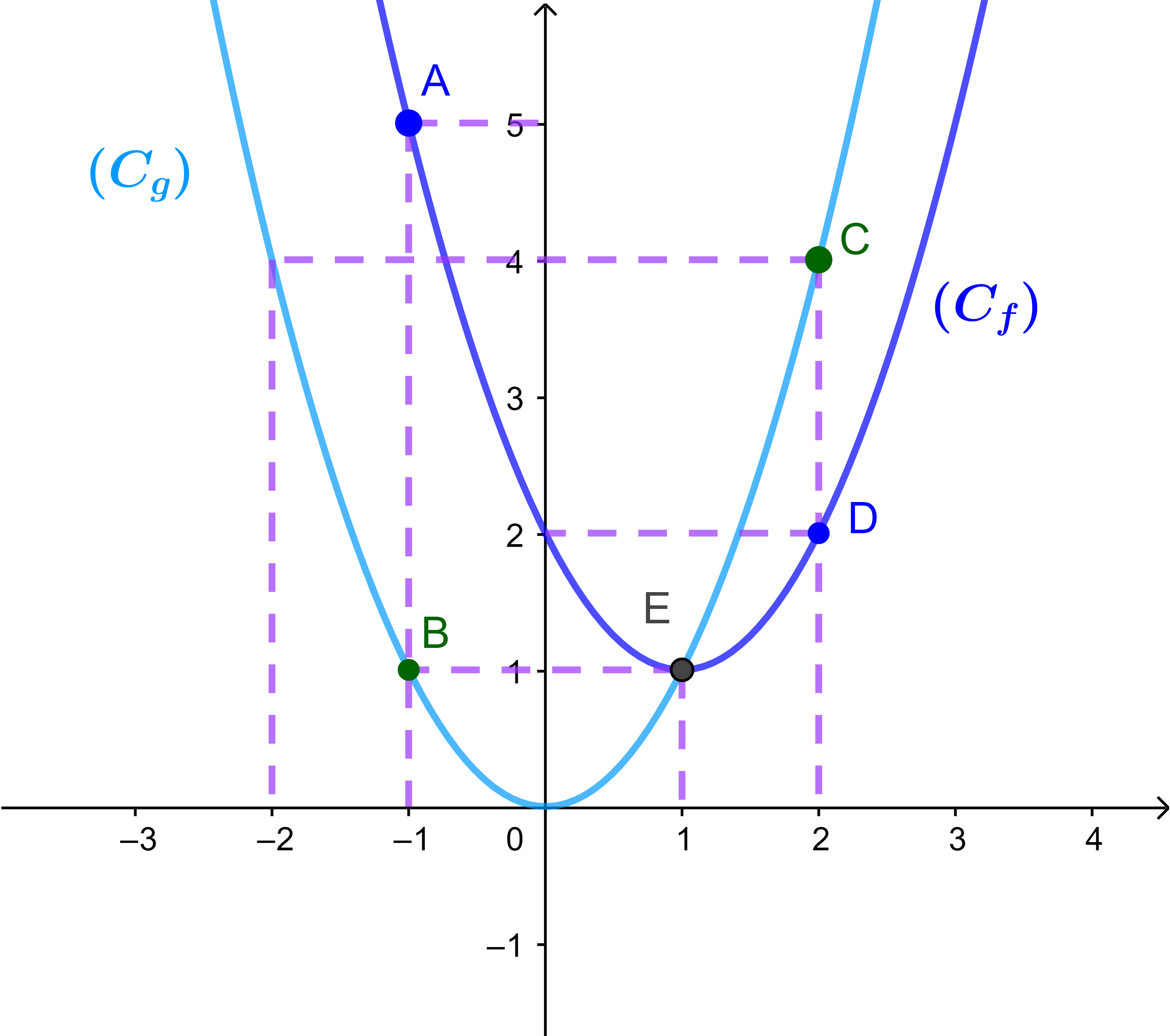
منحنيا الدالتين يلتقيان في نقطة واحدة
E(1 ; 1) وهذا يعني ان الدالتين متساويتان اذا كان x = 1
(C_f) فوق (C_g) في المجال ]-∞ ; 1]
وهذا يعني أن f ≥ g
(C_f) تحت (C_g) في المجال [1 ; +∞[
وهذا يعني أن f ≤ g

تمرين 3 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) , لتكن f و g دالتين عدديتين
و (C_f) و (C_g) منحنيهما على التوالي

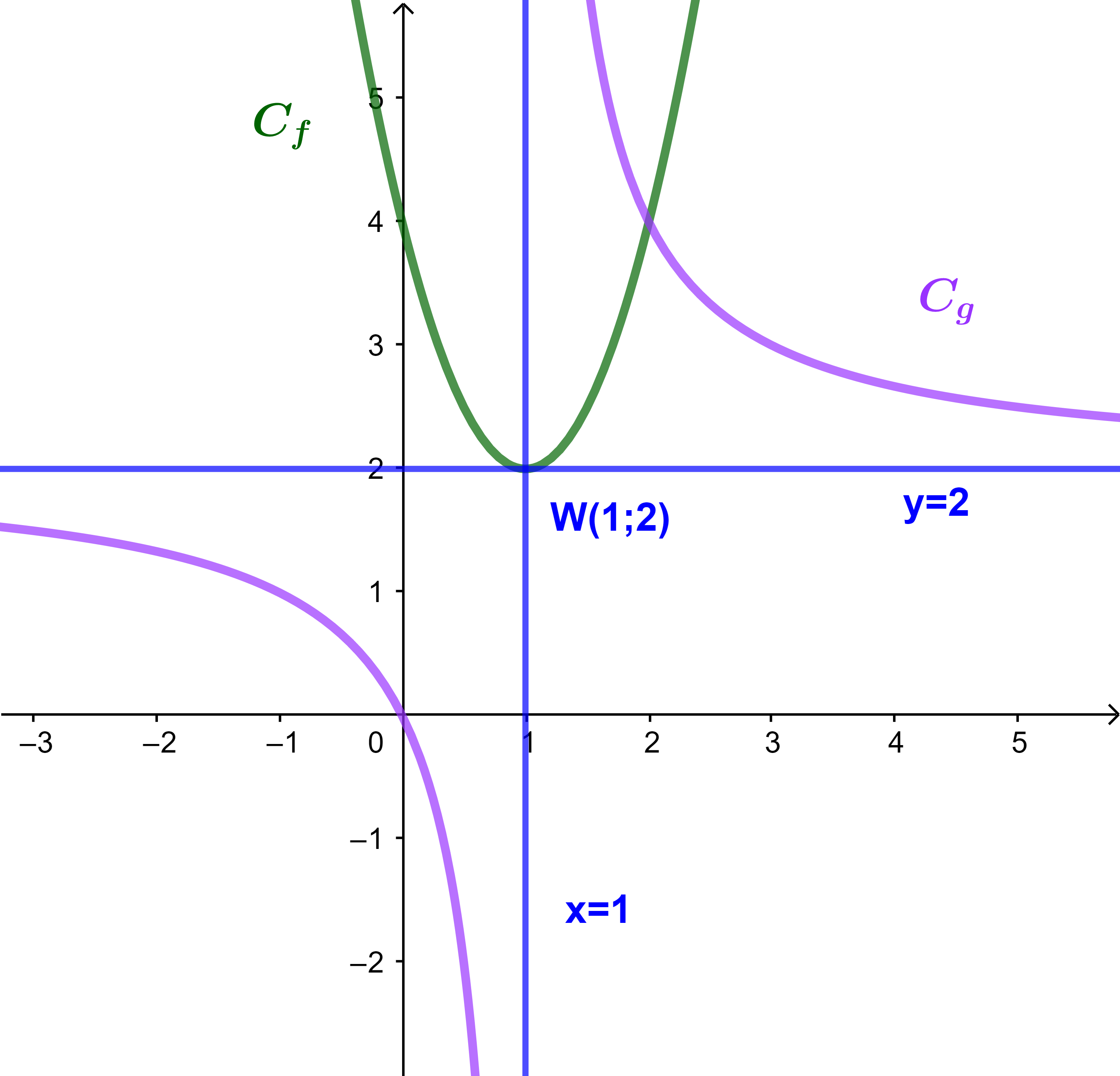
ادرس هندسيا اشارة الدالتين f و g

تصحيح

اشارة f
منحنى الدالة f فوق محور الافاصيل
اذن (∀x∈IR): f(x) ≥ 0
اشارة g
المستقيم (D): x = 1
يفصل منحنى الدالة g الى جزئين منفصلين
وهذا يعني ان الدالة g غير معرفة في 1
اذا كان x∈]-∞ ; 0] فان المنحنى (C_g) فوق محور الافاصيل
ومنه فان الدالة g موجبة على المجال ]-∞ ; 0]

اذا كان x∈[0 ; 1[ فان المنحنى (C_g) تحت محور الافاصيل
ومنه فان الدالة g سالبة على المجال [0 ; 1[
اذا كان x∈]1 ; +∞[ فان المنحنى (C_g) فوق محور الافاصيل
ومنه فان الدالة g موجبة على المجال ]1 ; +∞[
خلاصة الدالة g موجبة غلى اتحاد المجالين
]-∞;0]∪]1;+∞[ وسالبة على المجال [0;1[
ملاحظة اذا قطع منحنى دالة عددية f محور الافاصيل في نقطة ذات الافصول a فان f(a)=0.