للتذكير لتكن f دالة عددية معرفة على مجال I
1) نقول ان f مصغورة على المجال I اذا وجد عدد حقيقي m بحيث لكل x∈I لدينا f(x) ≥ m
وبتعبير آخر f مصغورة على I
يعني (∃m∈IR )(∀x∈I) (f(x) ≥ m )
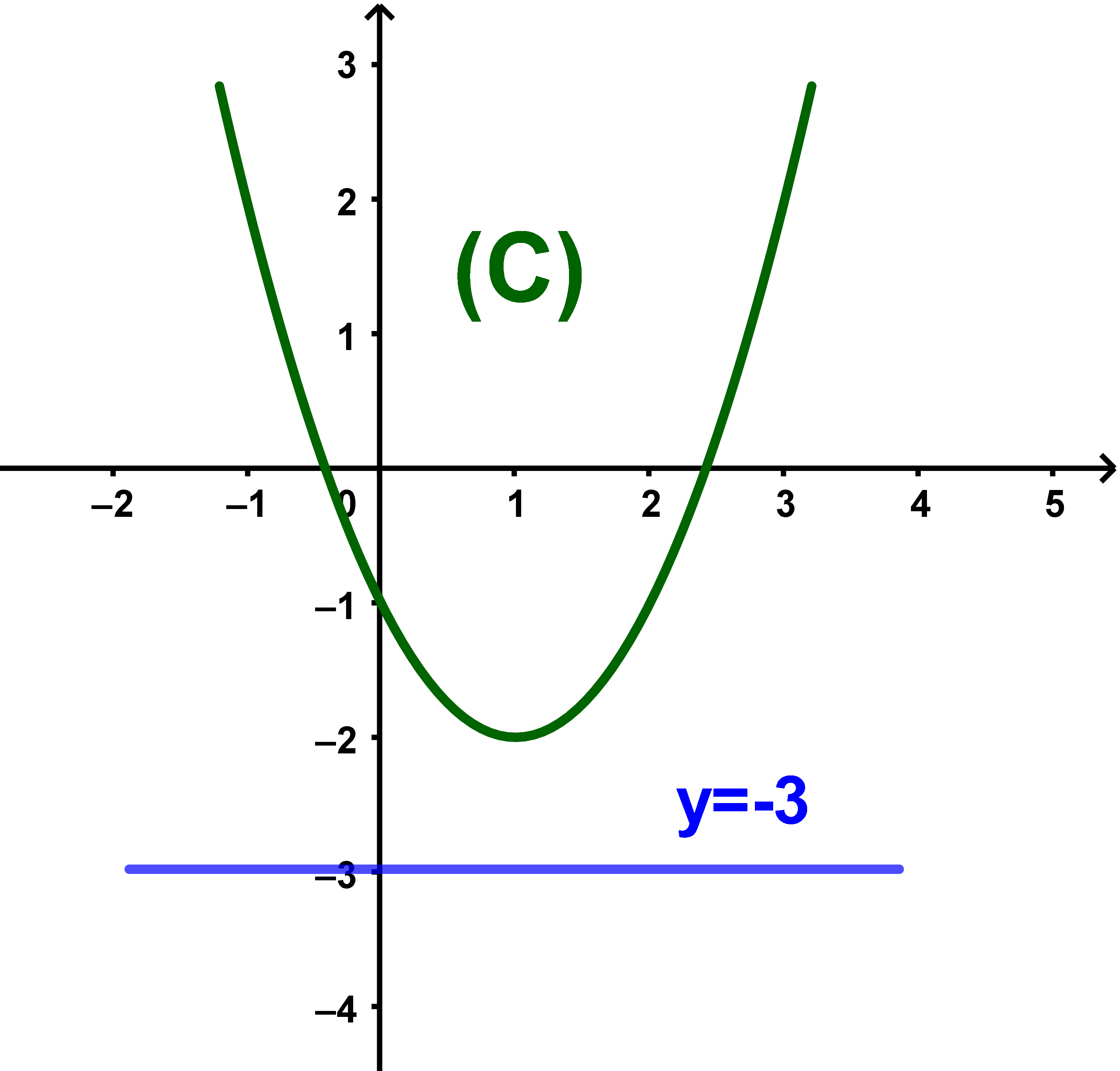
ملاحظة اذا كانت f دالة مصغورة بعدد m فان (C) منحنى الدالة f يكون فوق المستقيم
الذي معادته y=m.

تمرين 1 tp

لتكن f دالة عددية معرفة كما يلي
f(x) = x² - 2x - 1.
1) بين ان (∀x∈IR) ( f(x)≥-2 ).

2) استنتج أن الدالة مصغورة
3) الدالة مصغورة بالعدد -3 ?

تصحيح

1) ليكن x∈IR
ندرس اشارة f(x) - (-2)
f(x) + 2 = x² - 2x - 1 + 2
= x² - 2x + 1 = (x - 1)²
(x - 1)² ≥ 0 اذن (∀x∈IR) ( f(x) ≥ -2 )
2) بما أن (∀x∈IR) ( f(x) ≥ - 2 )
فان الدالة f مصغورة بالعدد -2.

3) وأي عدد أصغر من -2 تكون الدالة f مصغورة به أيضا
-3 ≤ -2 اذن الدالة f مصغورة بالعدد -3.

تمرين 2 tp

لتكن f دالة عددية معرفة كما يلي
f(x) = x² + 5
بين ان f دالة مصغورة بالعدد 4.

تصحيح

ليكن x∈IR
f(x) - 4 = x²+ 5 - 4
= x² + 1
وبما أن ( ∀x∈IR ) ( x²+1 > 0)
فان ( ∀x∈IR ) ( f(x) > 4 )
وهذا يعني ان الدالة f مصغورة بالعدد 4

للتذكير لتكن f دالة عددية معرفة على مجال I
1) نقول ان f مكبورة على المجال I اذا وجد عدد حقيقي M بحيث لكل x∈I لدينا f(x) ≤ M
وبتعبير آخر f مكبورة على I
يعني (∃M∈IR )(∀x∈I) (f(x) ≤ M )
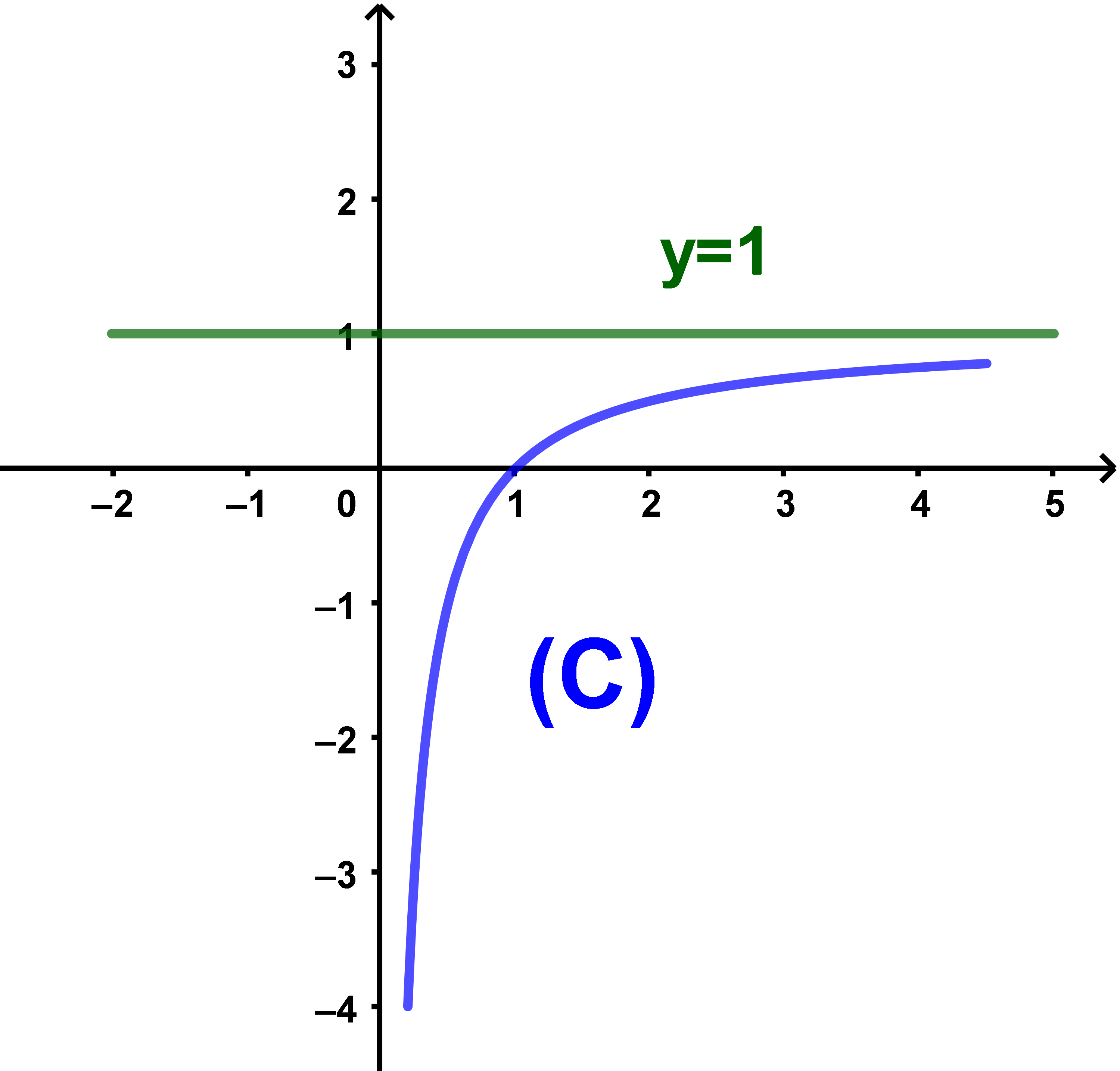
ملاحظة اذا كانت f دالة مكبورة بعدد M فان (C) منحنى الدالة f يكون تحت المستقيم الذي معادته y = M
نقول ان دالة f محدودة على مجال I اذا كانت مصغورة ومكبورة في آن واحد على I

تمرين 3 tp

لتكن f دالة عددية معرفة كما يلي

f(x) = 1 -	1
	x

بين ان (∀x∈IR^+*) (f(x) < 1)

تصحيح

ليكن x∈IR^+* اذن x≠0
وبالتالي f معرفة على IR^+*
نبين ان (∀x∈IR^+*) (f(x) - 1 < 0) ?

f(x) - 1 =	-1	< 0
	x

وهذا يعني ان (∀x∈IR^+*) (f(x) < 1)

تمرين 4 tp

بين ان الدالة العددية f المعرفة كما يلي
f(x) = -x²+1 مكبورة بالعدد 2

تصحيح

ليكن x∈IR f(x) - 2 = -x² + 1 - 2
= -x² - 1 = - (x² + 1)
- (x² + 1) < 0
اذن (∀x∈IR)( f(x)<2
وهذا يعني ان الدالة f مكبورة بالعدد 2.