Rappel Soient f et g deux fonctions numériques définies sur un intervalle I et C_f) et (C_g) leurs courbes respectives dans un repère
1) f < g ⇔(C_f) est au-dessous de (C_g) sur I
2) f > g ⇔(C_f) est au-dessus de (C_g) sur I.

Exercice 1 tp

Le plan est rapporté à un repère orthonormé
(O ; i^→ ; j^→). Soient f et g deux fonctions
définies par f(x) = x + 3 et g(x) = x + 1
Tracer (C_f) et (C_g) sur un même repère et déduire leur position relative.

Correction

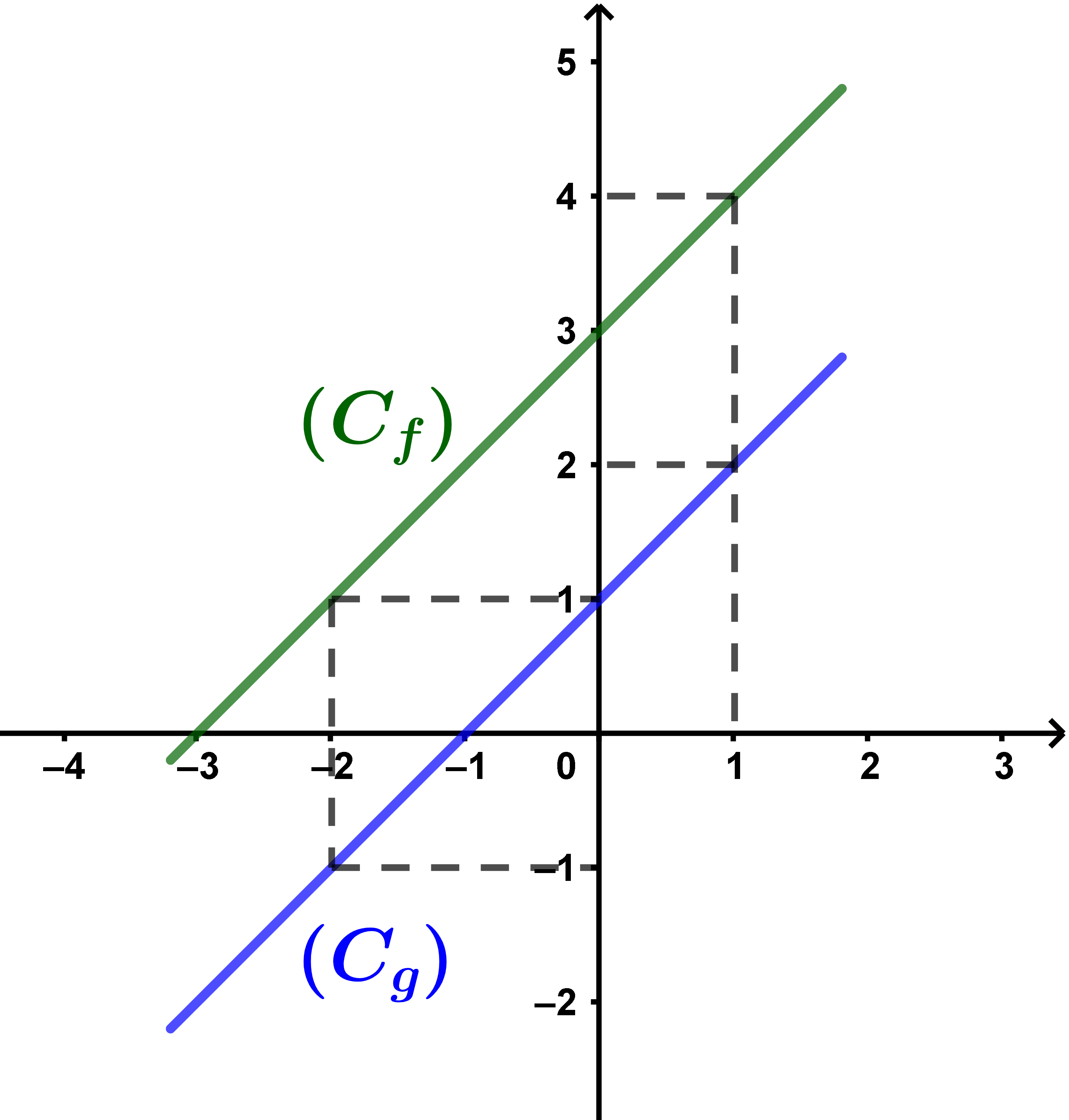
(C_f) est au dessus de (C_g)
Et donc f > g sur IR

Exercice 2 tp

Le plan est rapporté à un repère orthonormé
(O ; i^→ ; j^→). Soient f et g deux fonctions
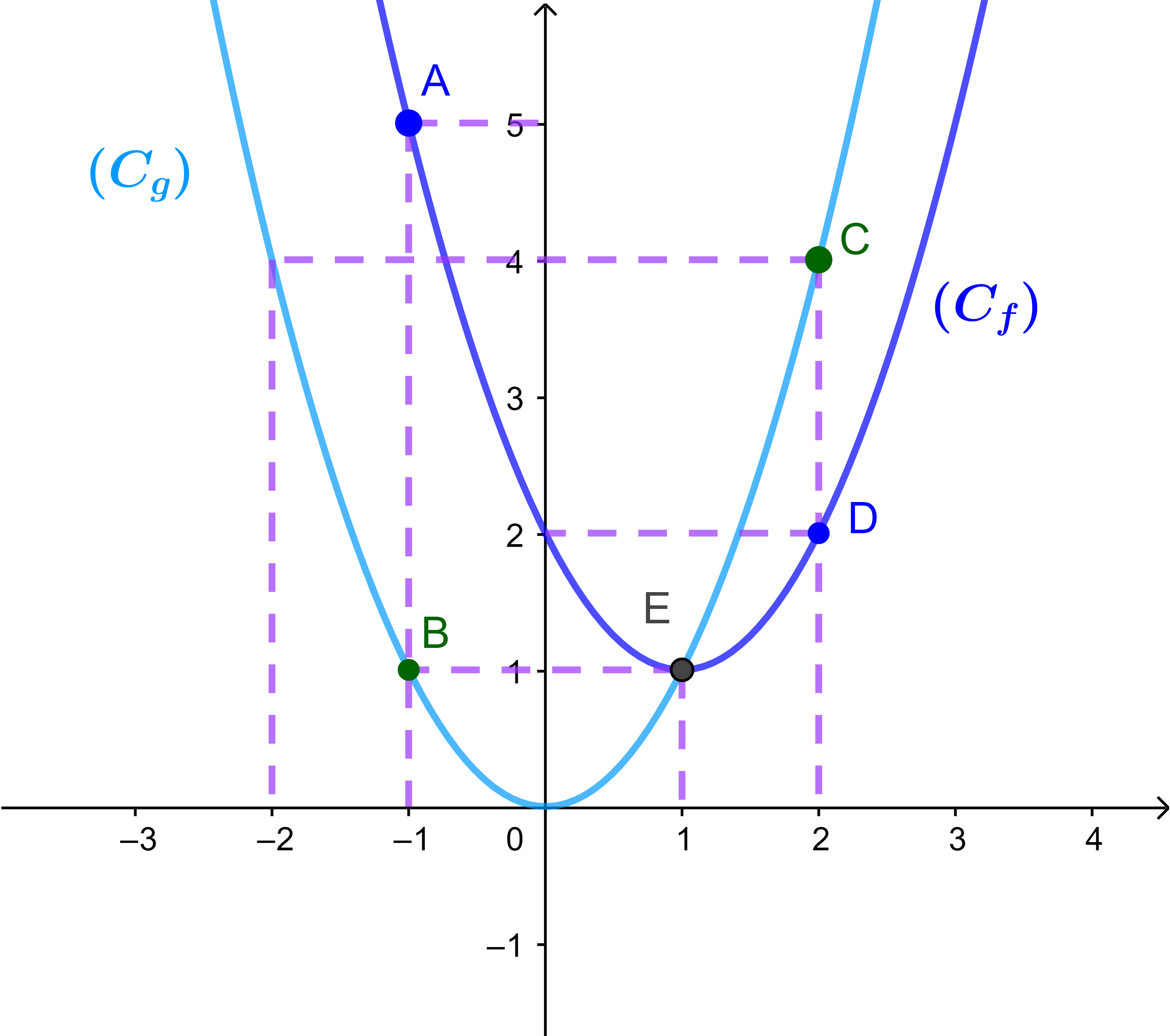
définies par f(x)= x²-2x+2 et g(x) = x²
Comparer algébriquement et géométriquement f et g

Correction

1) On compare algébriquement f et g
On étudie le signe de f(x)-g(x)
f(x) - g(x) = x²-2x+2 - x² = -2x+2
f(x) - g(x) = 0 ⇔ -2x+2 = 0 ⇔ x=1
donc f = g si x = 1

f(x) - g(x) > 0 ⇔ -2x+2>0 ⇔ -2x > -2
⇔ 2x < 2 ⇔ x < 1
donc f > g sur ]-∞ ; 1[
f(x) - g(x) < 0 ⇔ -2x+2 < 0 ⇔ -2x < -2
⇔ 2x > 2 ⇔ x > 1
donc f < g sur ]1 ; +∞[
2) On compare f et g géométriquement
(C_f) et (C_g) se coupent en un seul point,
E(1 , 1) donc f = g si x=1
Si x∈]-∞ ; 1] la courbe (C_f) est au-dessus de (C_g)
donc f > g sur ]-∞ ; 1[

Si x∈]1 ; +∞[ la courbe (C_f) est au-dessous de (C_g) donc f < g sur ]1 ; +∞[

Exercice 3 tp

Soient f et g deux fonctions numériques et (C_f) et (C_g) leurs courbes représentatives

Etudier graphiquement le signe de f et g

Correction

1) Signe de f
la courbe (en verte) de la fonction f est au-dessus de l'axe des abscisses
Et cela signifie que f est positive sur IR
En d'autre terme (∀x∈IR): f(x)> 0
2) Signe de g
la droite (D) d'équation x=1 sépare la courbe (C_g) en deux parties disjointes
cela signifie que la fonction g n'est pas définie en 1

(i) Sur ]-∞ ; 0] la courbe (C_g) est au-dessus de l'axe (Ox)
donc g ≥ 0 sur ]-∞;0]
(ii) Sur [0 ; 1[ la courbe (C_g) est au dessous de l'axe (Ox)
donc g ≤ 0 sur [0;1[
(iii) Sur ]1;+∞[ la courbe (C_g) est au-dessus de l'axe (Ox)
donc g > 0 sur ]1;+∞[.