Rappel Soit f une fonction définie sur un intervalle I
1) f est minorée sur I s'il existe un nombre
m tel que (∀x∈I) on a f(x) ≥ m
Ou encore (∃m∈R) (∀x∈I) (f(x) ≥ m )
Remarque Si f est minorée sur I par un nombre m alors sa courbe (C) est au dessus de la droite d'équation y = m
2) f est majorée sur I s'il existe un nombre
M tel que (∀x∈I) on a f(x)≤M
ou encore (∃M∈R) (∀x∈I) (f(x)≤M ).

Remarque Si f est majorée sur I par un nombre M alors sa courbe (C) est au dessous de la droite d'équation y = M
3) f est bornée sur I si elle est à la fois majorée et minorée sur I

Exercice 1 tp

Soit f une fonction numérique définie par
f(x) = x² - 2x - 1
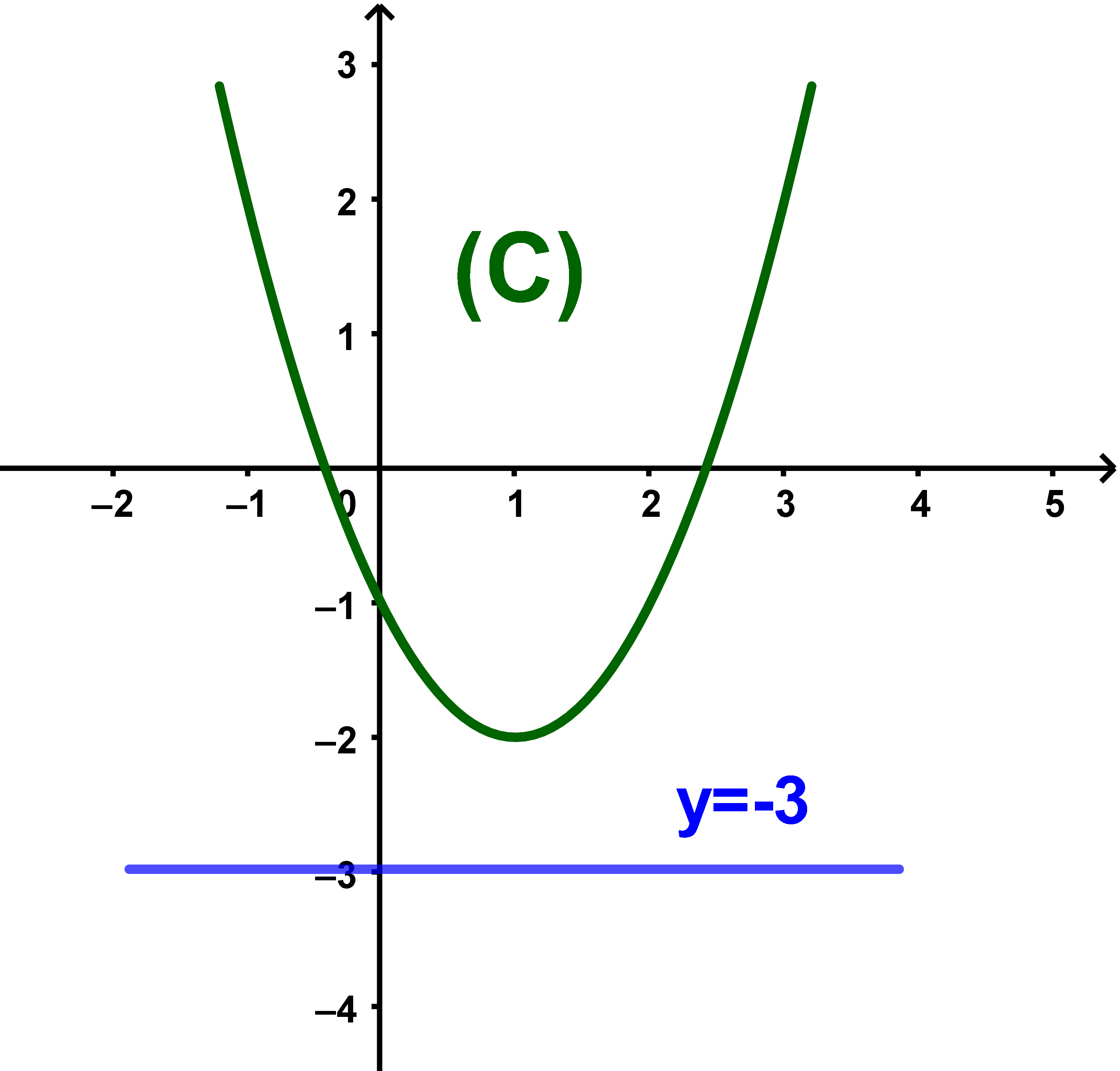
Montrer que f est minorée par -2

Correction

Soit x∈IR on étudie le signe de f(x) - (-2)
f(x) - (-2) = x² - 2x -1 + 2 = x² - 2x + 1

f(x) - (-2) = (x - 1)²≥0 donc (∀x∈IR) (f(x) > -2)
Ainsi f est minorée par -2

Exercice 2 tp

Soit f une fonction numérique définie
f(x) = x² + 5
Montrer que f est minorée par 4

Correction

Soit x∈IR
f(x) - 4 = x²+5 - 4 = x² + 1
Puisque (∀x∈IR) on a x²+1 > 0
alors (∀x∈IR): (f(x) > 4)
et cela signifie que f est minorée par 4

Exercice 3 tp

Soit f une fonction numérique définie par

f(x) = 1 -	1
	x

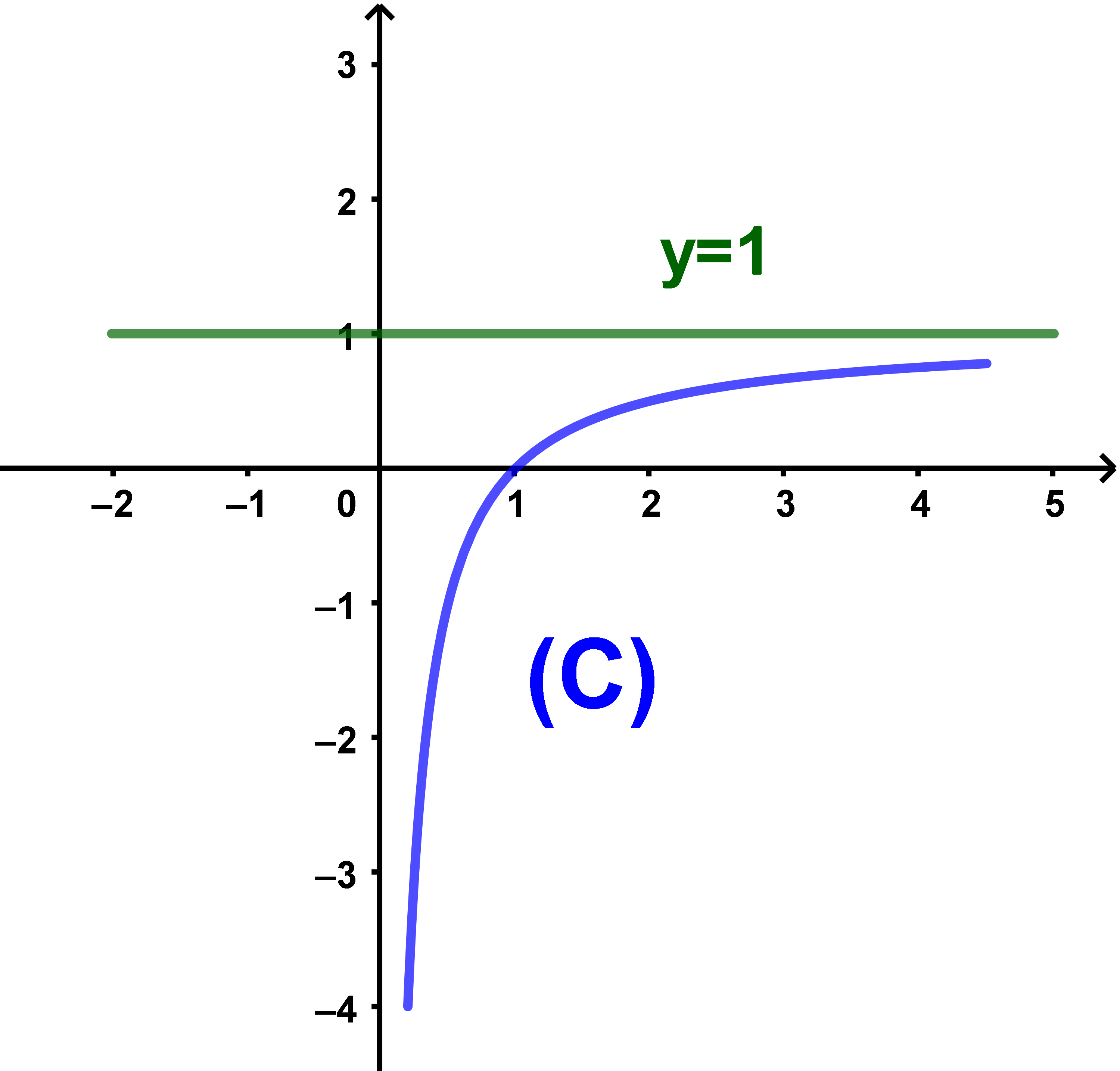
Montrer que majorée par 1

Correction

f fonction est définie si x≠0 donc D = IR*
Montrons que (∀x∈IR_+*) (f(x) - 1 < 0)

f(x) - 1 =	-1	< 0
	x

Signifie (∀x∈IR^+*) (f(x) < 1)
Donc f est majorée par 1

Exercice 4 tp

Soit f une fonction numérique définie
f(x) = -x² + 1
Montrer que f est majorée par 2

Correction

Soit x∈IR
f(x) - 2 = -x² + 1 - 2 = -x² - 1
= -(x² + 1)
Puisque (∀x∈IR) on a x² + 1 > 0
alors -(x² + 1) < 0
ainsi (∀x∈IR): (f(x) < 2)
et cela signifie que f est majorée par 2.