تمرين 1 tp

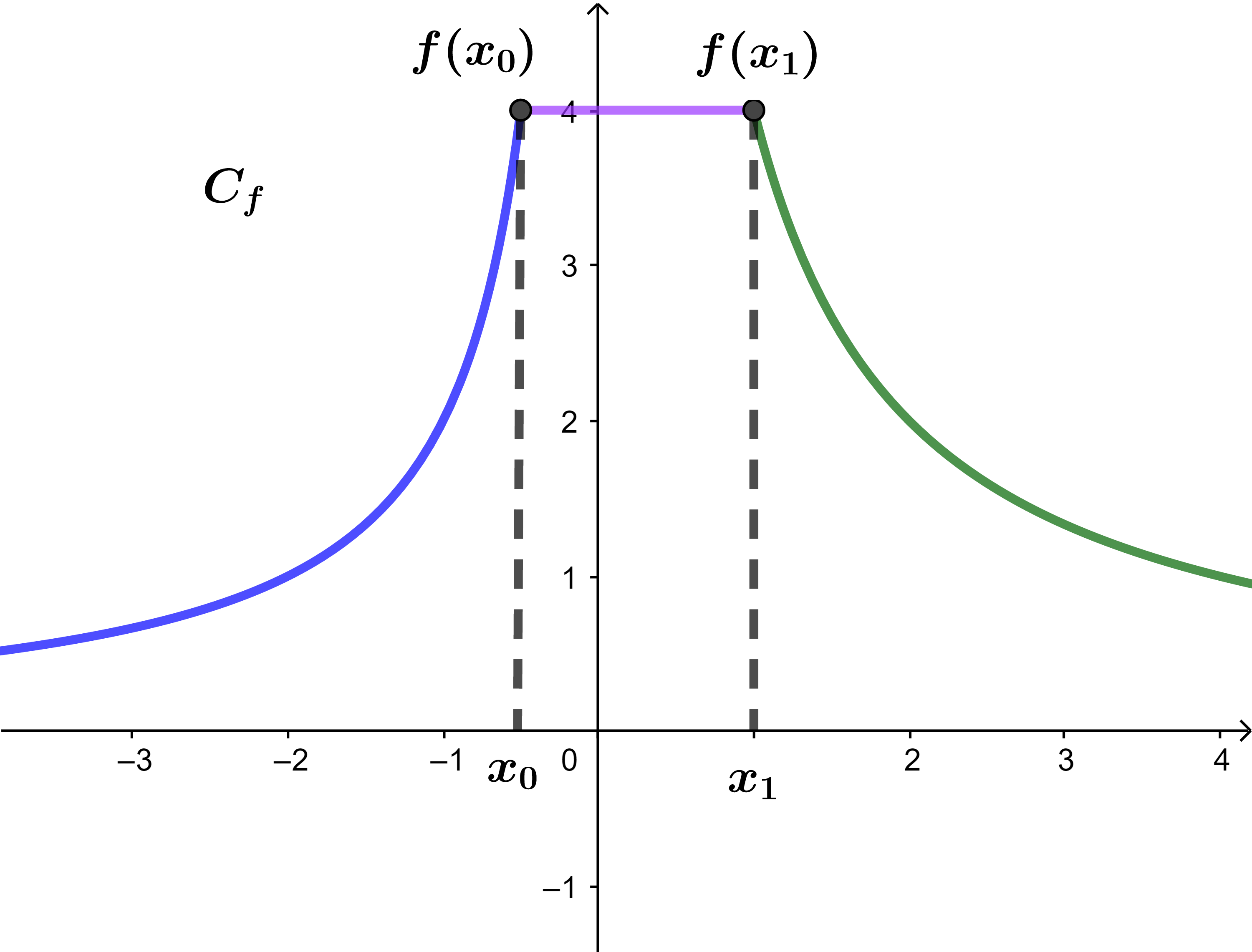
لتكن f دالة عددية و (C المنحنى الممثل لها في معلم
حدد مبيانيا رتابة الدالة f في كل من المجالات التالية
]-∞;x₀] ; [x₀;x₁] ; [x₁;+∞[.

تصحيح

f تزايدية قطعا على ]-∞;x₀] وثابتة على [x₀ ; x₁] وتناقصية قطعا على [x₁ ; +∞[

x	-∞		x0		x1		+∞
f		↗		----		↘

تمرين 2 tp

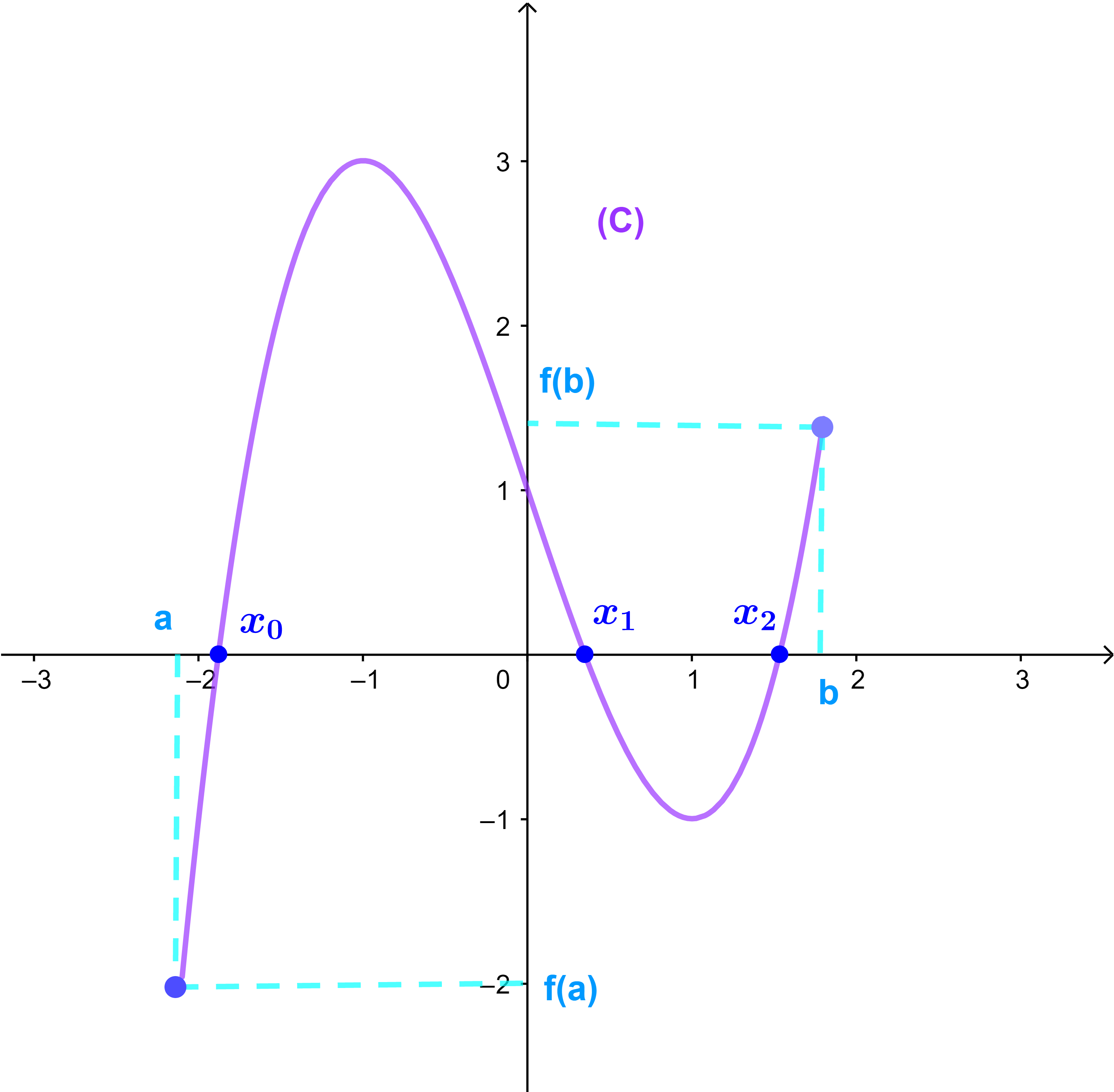
لتكن f دالة عددية معرفة مبيانيا على المجال [a;b]
1) حدد صورة بالدالة f كل من -2; -1; 1
حدد سوابق العدد 0
2) حل مبيانياالمعادلة f(x) = 0

3) اطر حلول المعادلة التالية f(x) = 2
4) حل مبيانيا المتراجحة f(x) ≥ 0
5) حدد تغيرات الدالة f على [a;b] وانشئ جدول تغيراتها

تمرين 3 tp

f دالة عددية معرفة كما يلي

f(x) =	3x
	x+1

1) حدد D_f
2) ادرس تغيرات الدالة f على ]-∞ ; -1[
ثم على ]-1 ; +∞[
3) انشئ جدول تغيرات الدالة f
4) حل في IR المعادلة f(x) = x²-x

تصحيح

1) D = {x∈IR / x+1≠0}
نحل المعادلة x+1= 0 اي x=-1
اذن D=IR\{-1}=]-∞ ; -1[∪]-1 ; +∞[
2) تغيرات الدالة f
ليكن x;y∈D حيث x ≠ y ندرس اشارة معدل التغير T(x ; y)

T(x ; y) =	f(x) - f(y)
	x - y

اولا نحسب f(x) -f(y)

f(x) - f(y) =	3x	-	3y
	x+1		y+1

=	3x(y+1) - 3y(x+1)	=	3(x-y)
	(x+1)(y+1)		(x+1)(y+1)

بالاختزال ب x-y نحصل على T(x ; y)

T(x ; y) =	3
	(x+1)(y+1)

ومنه فان اشارة T(x ; y) هي اشارة (x+1)(y+1)

ندرس تغيرات الدالة f على ]-∞ ; -1[
ليكن x;y∈]-∞ ; -1[ اذن
x < -1 اي x+1 < 0
y < -1 اي y+1 < 0

ومنه فان (x+1)(y+1) > 0
اذن T(x ; y) > 0 وهذا يعني ان f دالة تزايدية قطعا على ]-∞ ; -1[
ليكن x;y∈]-1 ; +∞[ اذن
x > -1 اي x+1 > 0
y > -1 اي y+1 > 0
ومنه فان (x+1)(y+1) > 0
اذن T(x ; y) > 0 وهذا يعني ان f دالة تزايدية قطعا على ]-1 ; +∞[

3) جدول تغيرات f

x		-∞		-1			+∞
f			↗			↗

4) نحل في D المعادلة f(x) = x²-x
f(x) = x²-x يعني 3x = (x+1)(x²-x)
يعني x³-x²+x²-x-3x = 0
x³-4x=0 يعني x(x²-4) = 0
يعني x=0 او x²=4
يعني x=0 او x=-2 او x=2
وبما ان -2 ; 0 ; 2 ∈D
فان S={-2 ; 0 ; 2}.