Exercice 1 tp

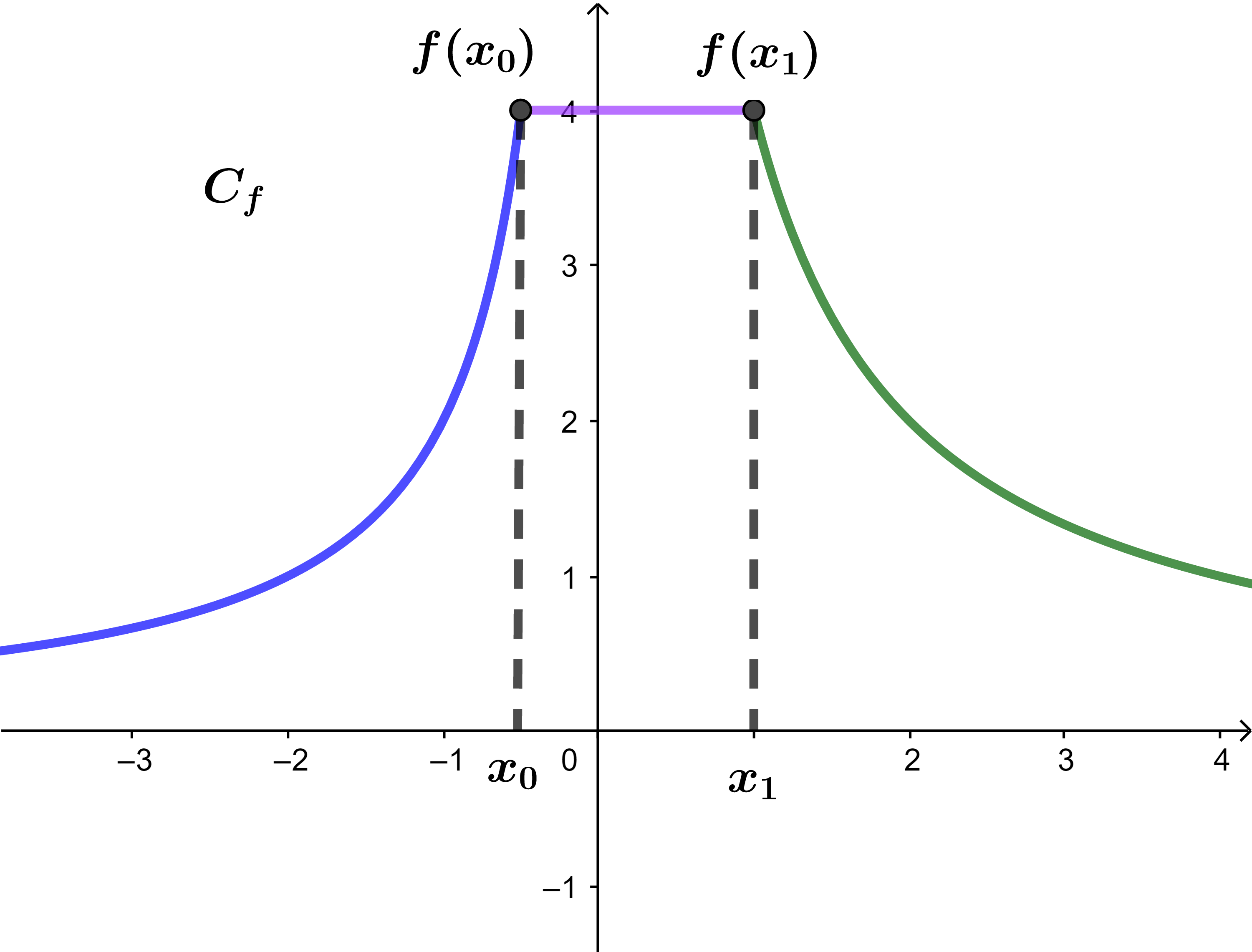
Soit f une fonction et (C) sa courbe
Déterminer graphiquement les variations de f
sur ]-∞;x₀] ; [x₀;x₁] ; [x₁;+∞[ .

Correction

1) f est croissante sur l'intervalle ]-∞ ; x₀]
2) f est constante sur l'intervalle [x₀ ; x₁]
3) f est décroissante sur l'intervalle [x₁ ; +∞[.

x	-∞		x0		x1		+∞
f		↗		----		↘

Exercice 2 tp

Soit f une fonction numérique
définie graphiquement sur [a;b]
1) Déterminer l'image par f de chacun des nombres -2 ; -1 et 1

Et déterminer les antécédents de 0

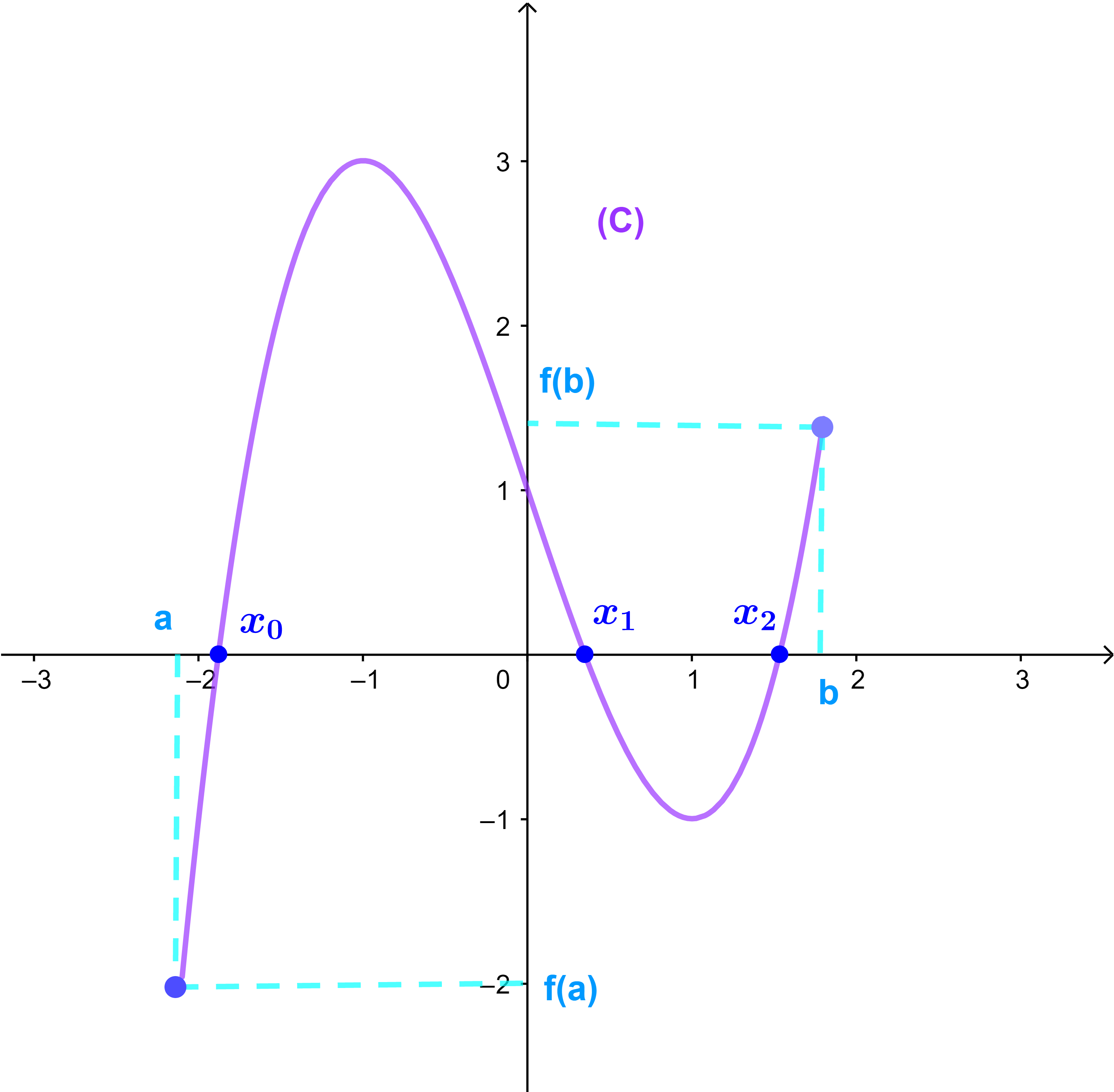
2) Résoudre graphiquement l'équation f(x) = 0
3) Encadrer les solutions de l'équation f(x) = 2

4) Résoudre graphiquement
l'inéquation f(x) ≥ 0
5) Etudier la monotonie de f sur [a;b] et tracer son tableau de variations

Exercice 3 tp

Soit f une fonction définie par

f(x) =	3x
	x + 1

1) Etudier la monotonie de f
sur ]-∞ -1[ puis sur ]-1 ; +∞[ et tracer son tableau de variations

2) Résoudre dans IR l'équation
f(x) = x²-x

Correction

1) f est définie si x+1≠0
x+1=0 ⇔ x=-1
Donc D = IR \{-1} = ]-∞ ; -1[∪]-1 ; +∞[
Soient x;y∈D tels que x≠y

f(x) - f(y) =	3x	-	3y
	x+1		y+1

=	3x(y+1)-3y(x+1)
	(x+1)(y+1)
=	3(x-y)
	(x+1)(y+1)

Donc le taux d'accroissement de f entre x et y

T(x ; y) =	f(x)- f(y)	=	3
	x-y		(x+1)(y+1)

Donc T(x ; y) est de signe (x+1)(y+1)

(a) Si x;y∈]-∞ ; -1[ alors x < -1 et y < -1
ou encore (x+1) < 0 et (y+1) < 0
donc (x+1)(y+1) > 0
ainsi T(x ; y) > 0 car 3 > 0
alors f est strictement croissante sur ]-∞ ; -1[
(b) Si x;y∈]-1 ; +∞[ alors x > -1 et y > -1
ou encore (x+1) > 0 et (y+1) > 0
donc (x+1)(y+1) > 0
ainsi T(x ; y) > 0 car 3 > 0
alors f est strictement croissante sur ]-1 ; +∞[

Tableau de variations

x		-∞		-1		+∞
f			↗		↗

4) Soit x∈D
f(x) = x²-x ⇔ 3x = (x+1)(x²-x)
⇔ x³-x²+x²-x-3x = 0
⇔ x³-4x = 0 ⇔ x(x²-4) = 0
⇔ (x=0 ou x²=4)
⇔ (x=0 ou x=-2 ou x=2)
puisque -2; 0 ;2∈D alors S = {-2 ; 0 ; 2}.