1.3 Limite des inverse des fonctions usuelles en ±∞

1.3.1 Activité

Compléter le tableau et conclure

x		-∞	-104	10³	105	..	+∞
1		..	..	..	..	..	..
x
1		..	..	..	..	..	..
x²
1		..	..	..	..	..	..
x³

1.3.2 Résultat 1

1) Plus la valeur de x est élévée, plus la valeur de

1	ou	1
x		x²

diminue et se rapproche de 0, on écrit donc

lim +∞	1	= 0	lim +∞	1	= 0
	x			x²

n∈IN*			lim +∞	1	= 0
				xn

1.3.3 Résultat 2

Plus la valeur de x diminue, et se rapproche de -∞, plus la valeur de

1	ou	1
x		x²

se rapproche de 0 donc

lim -∞	1	= 0		lim -∞	1	= 0
	x				x²

			lim -∞	1	= 0	(n∈IN*)
				xn

Exemples

lim -∞	1	= 0
	x4
lim -∞	1	= 0
	x5

1.4 Limite de l'inverse de x→x² et x→xⁿen 0 tel que n pair

1.4.1 Propriétés

Soit n un entier naturel pair et non nul.

lim 0	1	= +∞
	x²
lim 0	1	= +∞
	xn

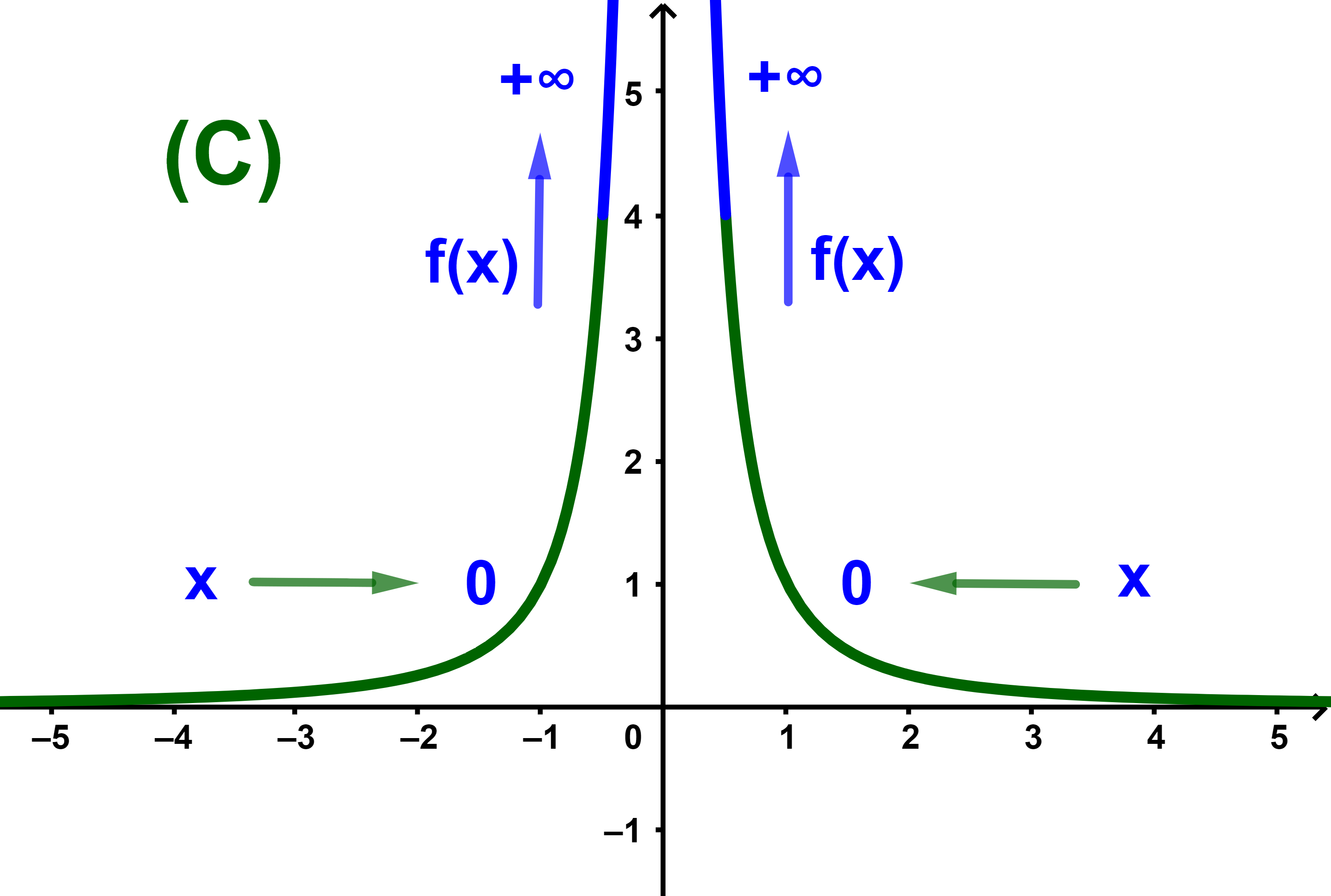
1.4.2 Exemple

lim 0	1	= +∞		lim 0	1	= +∞
	x4				x8

Exercice 1 tp

Soit f une fonction numérique définie par

f(x) =	1	+ 2
	x²

Calculer la limite suivante

lim 0

f(x)

Correction

On a

lim 0	f(x) - 2 =	lim 0	1	= +∞
			x²

donc

lim 0

f(x) = +∞