4- النهاية على اليمين والنهاية على اليسار

4.1 النهاية على اليمين

4.1.1 نشاط

لتكن f دالة عددية معرفة على المجال ]0;1[ بما يلي

f(x) =	1
	x

اتمم الجدول وحدد نهاية الدالة f عند 0 ان وجدت !

x	0	0,0001	0,001	0,01
f(x)	..	..	..	..

كلما اقترب x من 0 على اليمين كلما أخذت f(x) قيمة كبيرة تؤول الى +∞.

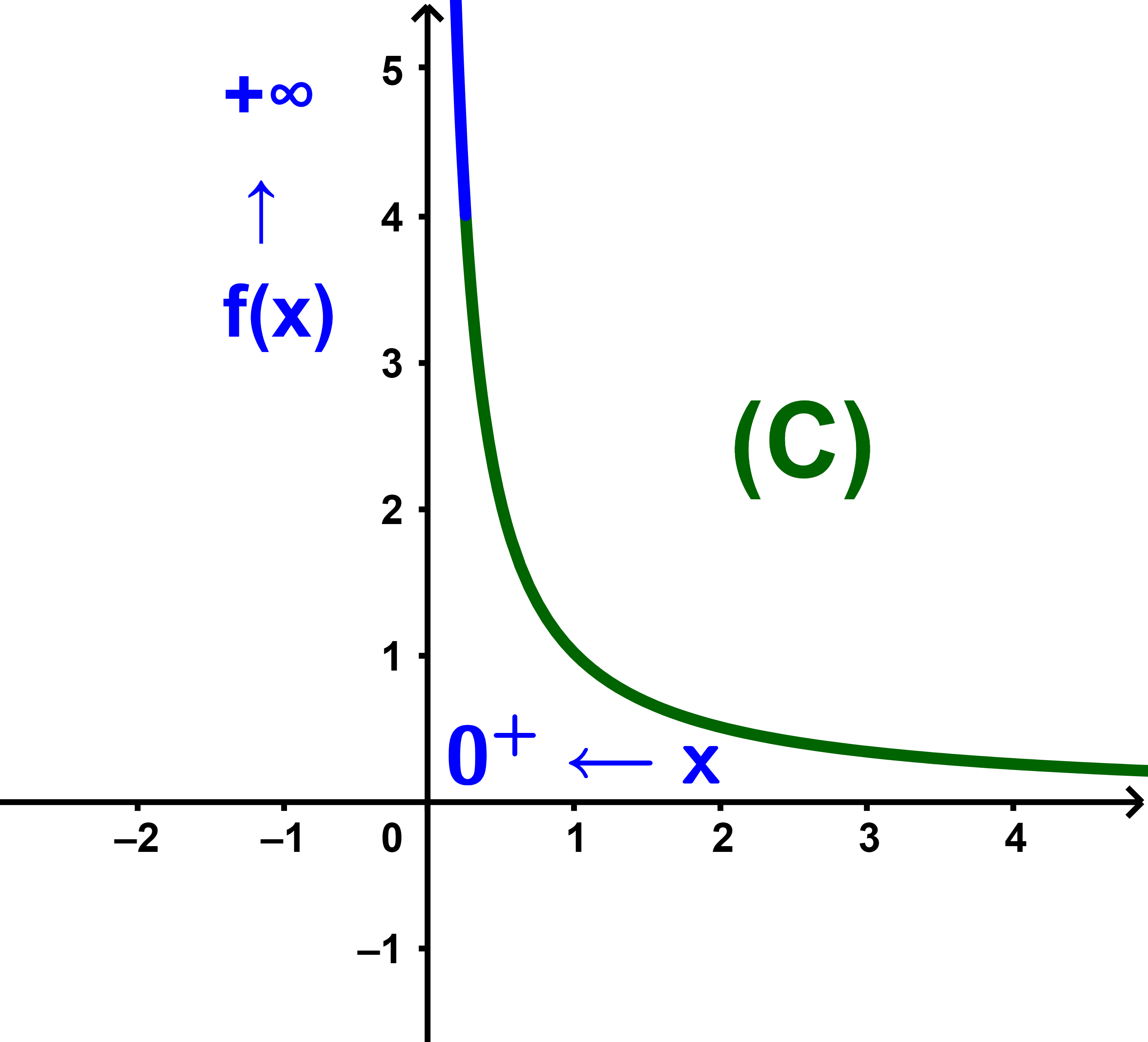
نقول ان نهاية f عند 0 على اليمين تساوي +∞ ونكتب

lim 0+	1	= +∞
	x

4.1.2 تعريف

لتكن f دالة عددية معرفة على مجال من نوع [a;a+α[ حيث α>0. اذا كانت f(x) تؤول الى L (±∞ او ) عندما x يؤول الى a على اليمين نكتب

lim x→a x>a

f(x) = L

أو نكتب

lim x→a+

f(x) = L

مثال 1

lim 1+	1	= ?
	x - 1

أولا ندرس اشارة x-1.

x		-∞		1		+∞
x - 1			-	0	+

اذن عندما x → 1⁺ فان x-1 → 0⁺

lim 1+	1	= +∞ اذن	1	= +∞
	x - 1		0+

4.2 النهاية على اليسار

4.2.1 نشاط

لتكن f دالة عددية معرفة على المجال ]-1;0[ بما يلي

f(x) =	1
	x

اتمم الجدول وحدد نهاية الدالة f عند 0 ان وجدت !

x	- 0,01	- 0,001	- 0,0001	0
f(x)	..	..	..	..

كلما اقترب x من 0 على اليسار كلما أخذت f(x) قيمة صغيرة تؤول الى -∞.

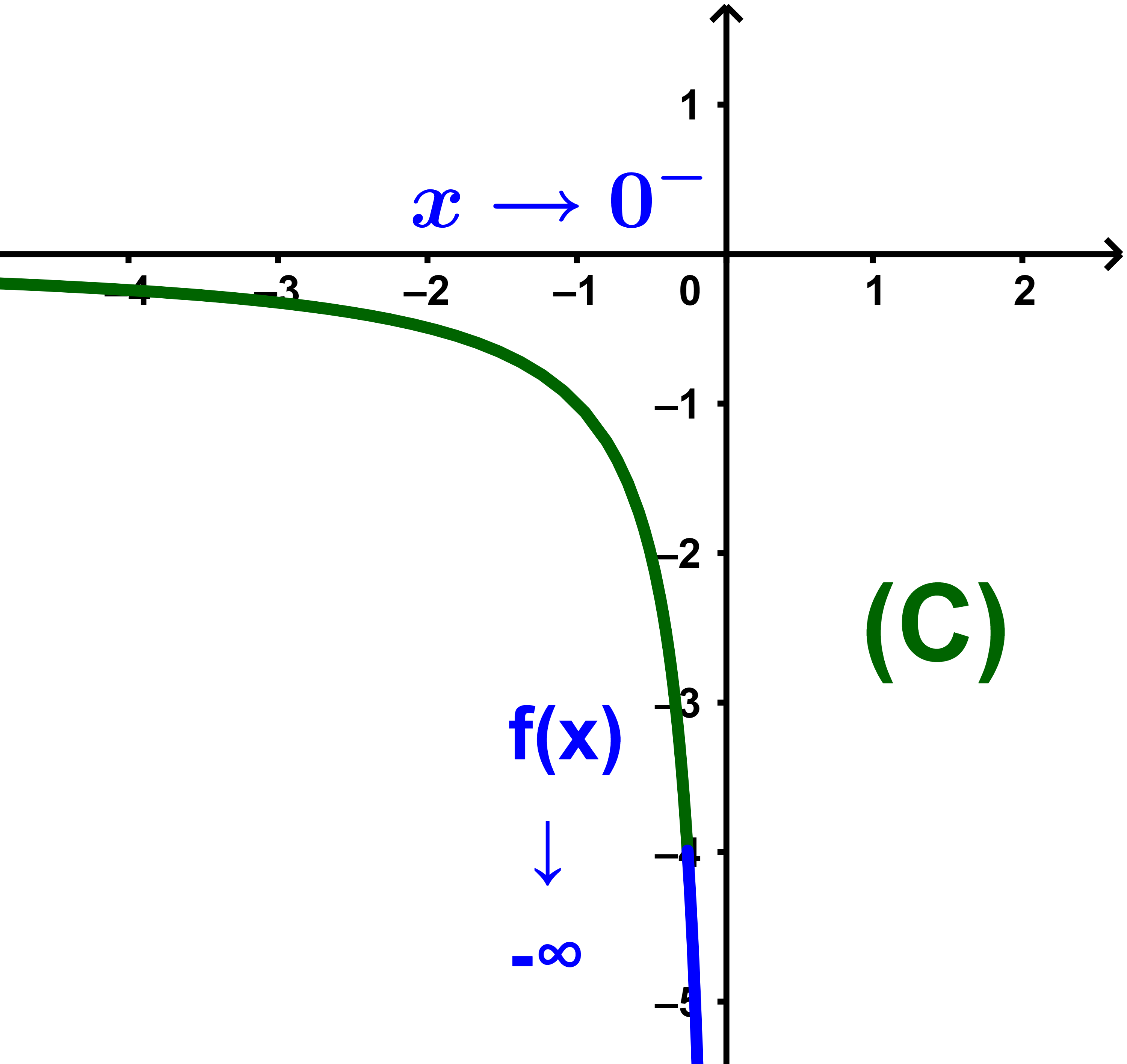
نقول ان نهاية f عند 0 على اليسار تساوي - ∞.

4.2.2 تعريف

لتكن f دالة عددية معرفة على مجال من نوع ]a-α;a] حيث α>0. اذا كانت f(x) تؤول الى L (±∞ او ) عندما x يؤول الى a على اليسار نكتب

lim x→a x < a

f(x) = L

أو نكتب

lim x→a-

f(x) = L

lim 2-	1	احسب	مثال
	5x - 10

أولا ندرس اشارة 5x-10.

x		-∞		2		+∞
5x - 10			-	0	+

اذن عندما x → 2^- فان 5x-10 → 0^-.

lim 2-	1	= - ∞ اذن	1	= - ∞
	5x - 10		0-

4.2.3 خاصيات

f تقبل نهاية عند عدد حقيقي a يعني ان نهايتها على اليمين تساوي نهايتها على اليسار عند a.