4- Limite à gauche et limite à droite

4.1 Limite à droite

4.1.1 Activité

Soit f une fonction définie sur ]0;+∞[ par

f(x) =	1
	x

Compléter le tableau suivant et conclure !

x	0	0,0001	0,001	0,01
f(x)	..	..	..	..

Plus la valeur de x se rapproche à droite à 0, plus la valeur de f(x) se rapproche de +∞.

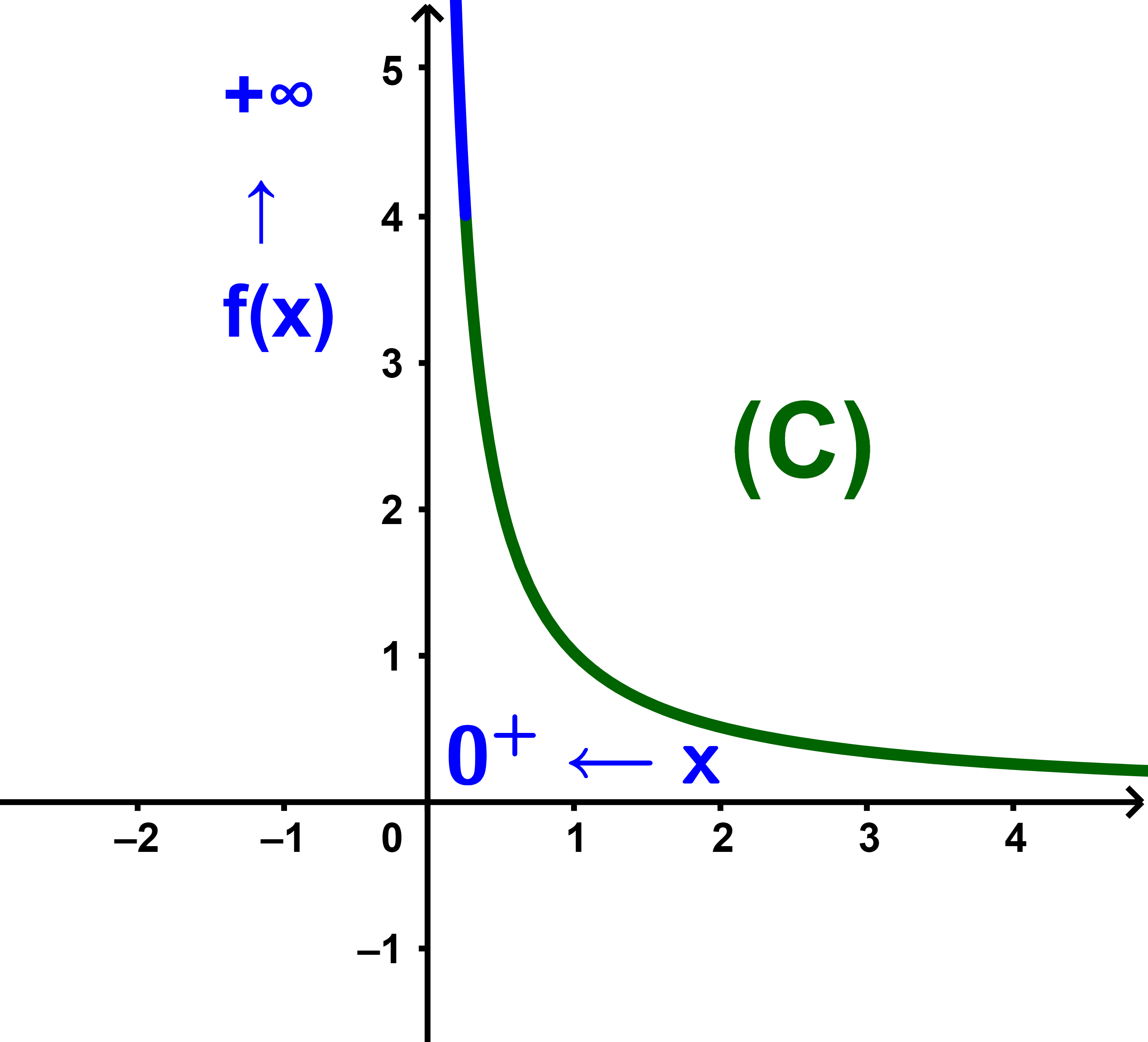
On écrit	lim 0+	1	= +∞
		x

4.1.2 Définition

Soit f une fonction définie sur un intérvalle sous la forme [a;a+r[ tel que r>0.
Si f(x) tend vers L (ou ±∞) quand x tend vers à droite à a, on écrit

lim x→a x>a

f(x) = L

ou

lim x→a+

f(x) = L

Exemple 1

lim 1+	1	= ?
	x - 1

On étudie le signe de x-1

x		-∞		1		+∞
x - 1			-	0	+

Si x → 1⁺ alors x-1 → 0⁺ ainsi

1	= +∞ ⇒	lim 1+	1	= +∞
0+			x - 1

4.2 Limite à gauche

4.2.1 Activité

Soit f une fonction définie sur ]-∞;0[ par

f(x) =	1
	x

Compléter le tableau suivant et conclure !

x	- 0,01	- 0,001	- 0,0001	0
f(x)	..	..	..	..

Plus la valeur de x se rapproche à gauche à 0, plus la valeur de f(x) se rapproche de -∞.

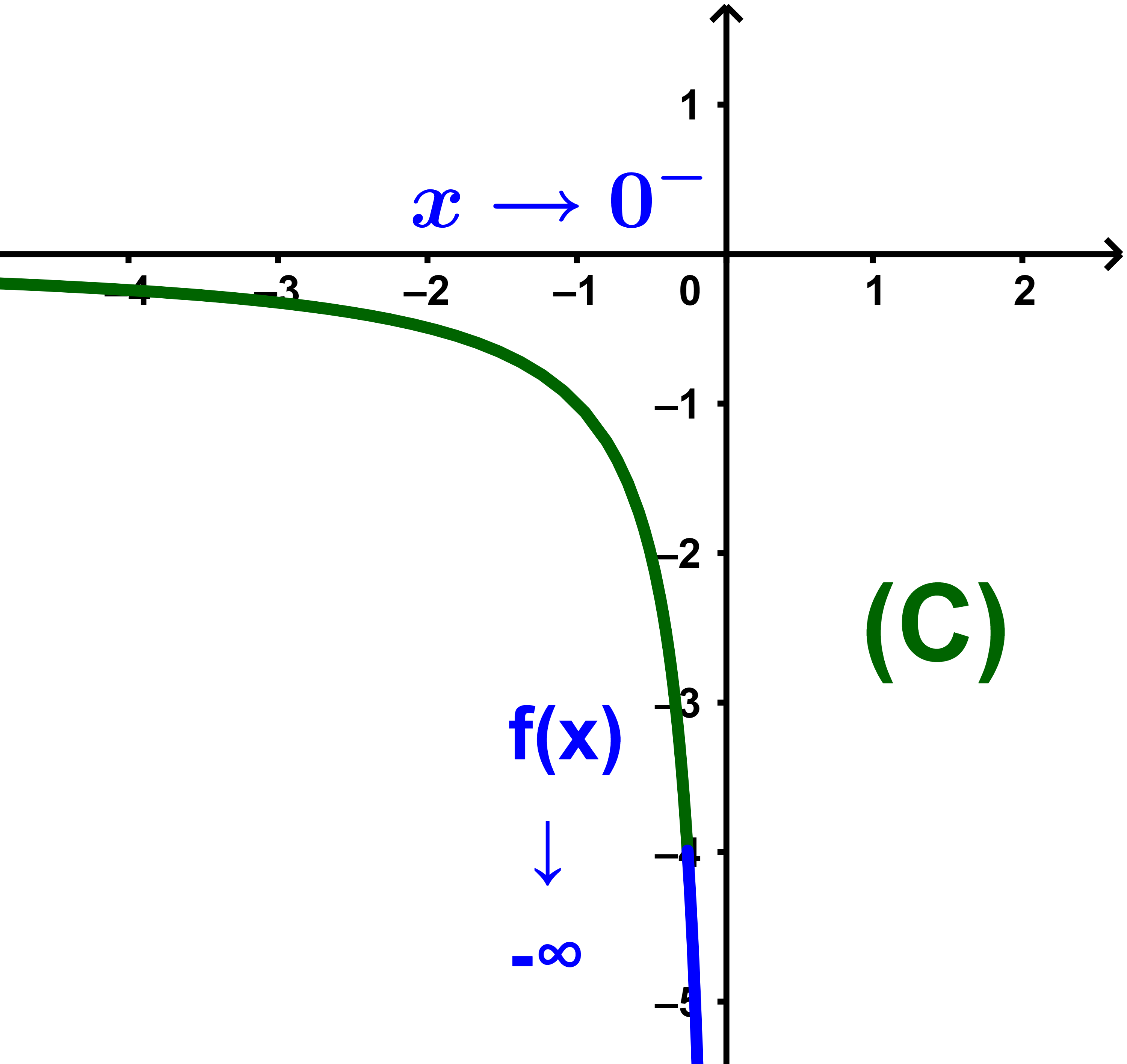
On écrit	lim 0-	1	= - ∞
		x

4.2.2 Définition

Soit f une fonction définie sur un intérvalle sous la forme ]a-r;a[ tel que r>0.
Si f(x) tend vers L (ou ±∞) quand x tend vers à gauche à a, on écrit

lim x→a x< a

f(x) = L

ou

lim x→a-

f(x) = L

Exemple

lim 2-	1	= ?
	5x - 10

Si x → 2^- alors 5x-10 → 0^- ainsi

1	= - ∞	⇒	lim 2-	1	= - ∞
0-				5x - 10

4.2.3 Propriétés

Une fonction admet une limite au point a signifie la limite à droite est égale à la limite à gauche au point a.