3- Les raisonnements mathématiques

Rappel
1) Une proposition est vraie ou fausse, pas les deux.
2) Si une proposition p est vraie et l'impliquation p⇒q est vraie alors la proposition q est également vraie.

Pratiquement pour montrer que p⇒q est vraie, il suffit de supposer que p est vraie et montrer que q est également vraie.

3.1 Raisonnement par l'absurde

Pour montrer qu'une proposition q est vraie, nous suivons les étapes suivantes
1) On suppose que q est fausse
sur la base de cette hypothèse nous obtenons une proposition p et sa négation ⌉p qui sont toutes les deux vraies, et ce n'est pas possible.
2) Nous concluons que l'hypothèse était fausse, ce qui signifie que la proposition q est vraie.

Exemple
Soit ABC un triangle tel que AB=5; BD=3; CE=2,25 et AC=4,25 ; E∈[AC] et D∈[AB]
Est ce que (DE)||(BC) ?

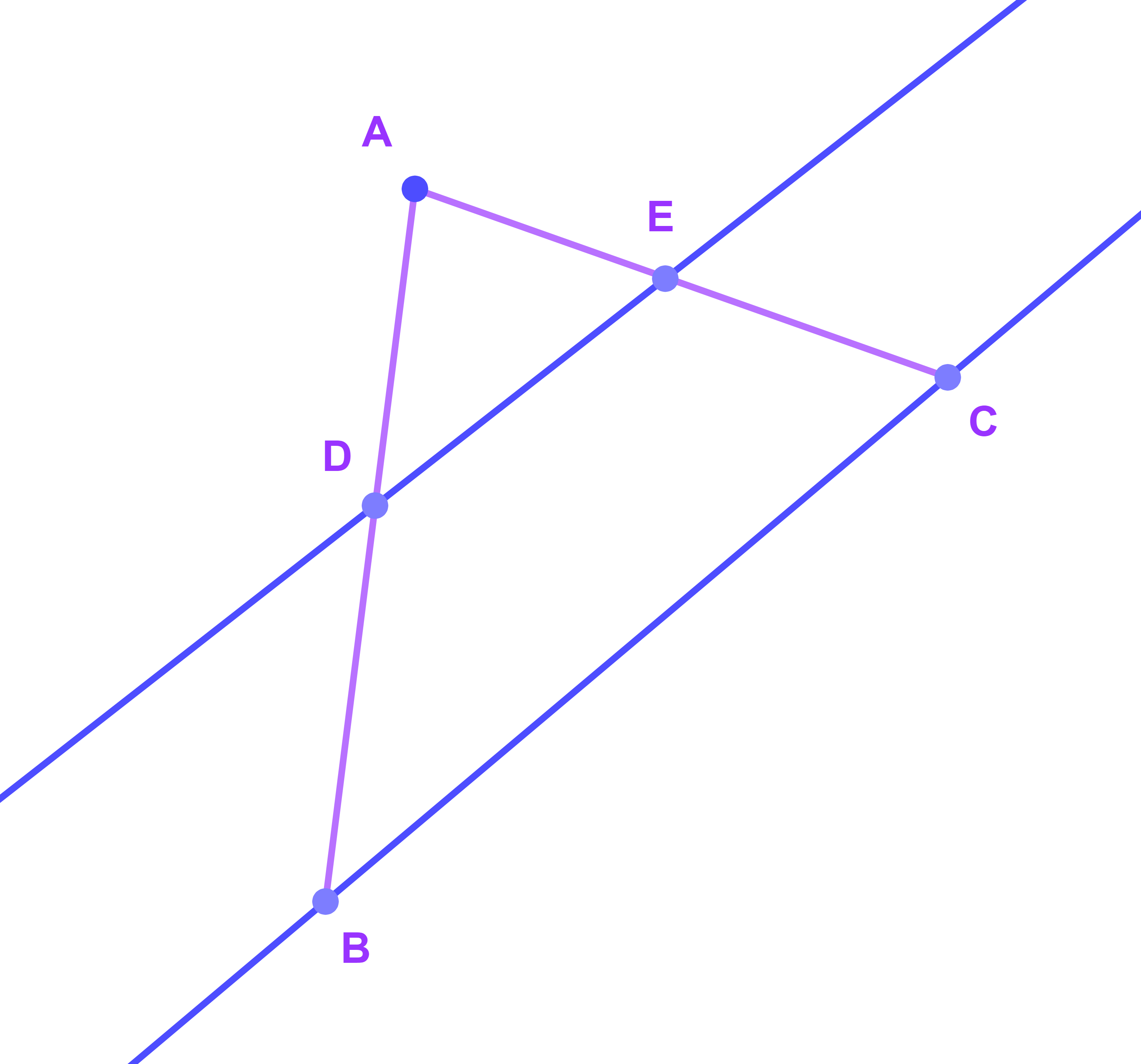
Nous supposons que (DE) et (BC) sont paralleles
d'après le théorème de Thalès, nous obtenons

⇔ 5,4×2,25=3×4,25
⇔ 12,15=12,75
et ce n'est pas possible.
Nous concluons donc que (DE) et (BC) ne sont pas parallèles.

3.3 Raisonnement par disjonction des cas

Pour montrer que (p⋁q)⇒r
on montre que p⇒r est vraie et q⇒r est aussi vraie
Pratiquement q=⌉p
et pour montrer que (p⋁⌉p)⇒r
il suffit de montrer p⇒r et ⌉p⇒r.

Exemple
Résoudre dans IR
l'équation (E): |x-2|=5

Correction
Le nombre x-2 peut être négatif ou positif
donc il y'a deux cas à discuter.
Si x-2 est positif ou encore x≥-2
alors |x-2|=x-2.
L'équation (E) devient donc x-2=5
et cela signifie que x=5+2=7 donc x=7.

Si x+2 est négatif ou encore x≤-2
alors |x+2|=-(x-2)=-x+2.
L'équation (E) devient donc -x+2=5
et cela signifie que -x=5-2 donc x=-3
ainsi l'ensemble des solutions de l'équation (E)
S={-3 ; 7}.