تمرين 1 tp

ليكن ABC مثلثا بحيث AB=25; AD=12; AE=14 ; AC=29 ; E∈[AC] ; F∈[AB]
هل (DE)||(BC) ? يمكن استعمال البرهان بالخلف

تصحيح

نستعمل البرهان بالخلف
نفترض ان المستقيمين متوازيان (DE)||(BC)
حسب مبرهنة طاليس ان

AB	=	AC
AD		AE

25	=	29
12		14

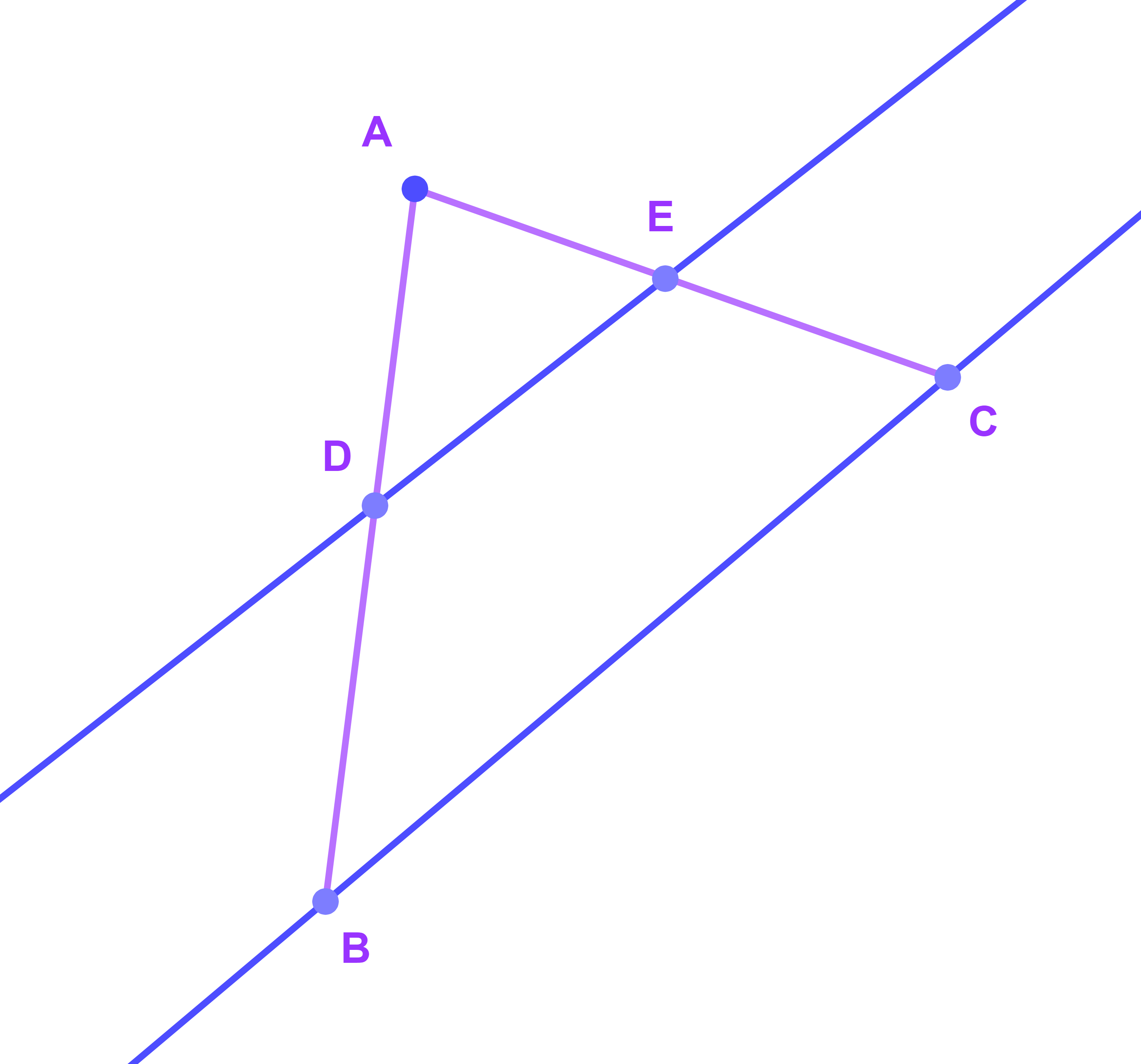
اي 25×14 = 12×29
اي 350 = 348 وهذا غير ممكن
نستنتج اذن ان المستقيمين (DE) و (BC)غير متوازيين

تمرين 2 tp

ليكن x∈E=]-∞ ; 0[
نضع

y =	x
	2-x

بين بالبرهان بالخلف ان (∀x∈E) : y ≥ -1

تصحيح

لدينا x < 0
اذن y < 0 لان (2-x > 0)

نفترض بالخلف ان y < -1
وهذا يعني ان

y =	x	< -1 ⇒ x < -(2-x) ⇒ 0 < -2
	2-x

وهذا غير ممكن وبالتالي (∀x∈E) : y≥-1.