La fonction exponentielle népérien (4)
2- Etude de la fonction x→ex
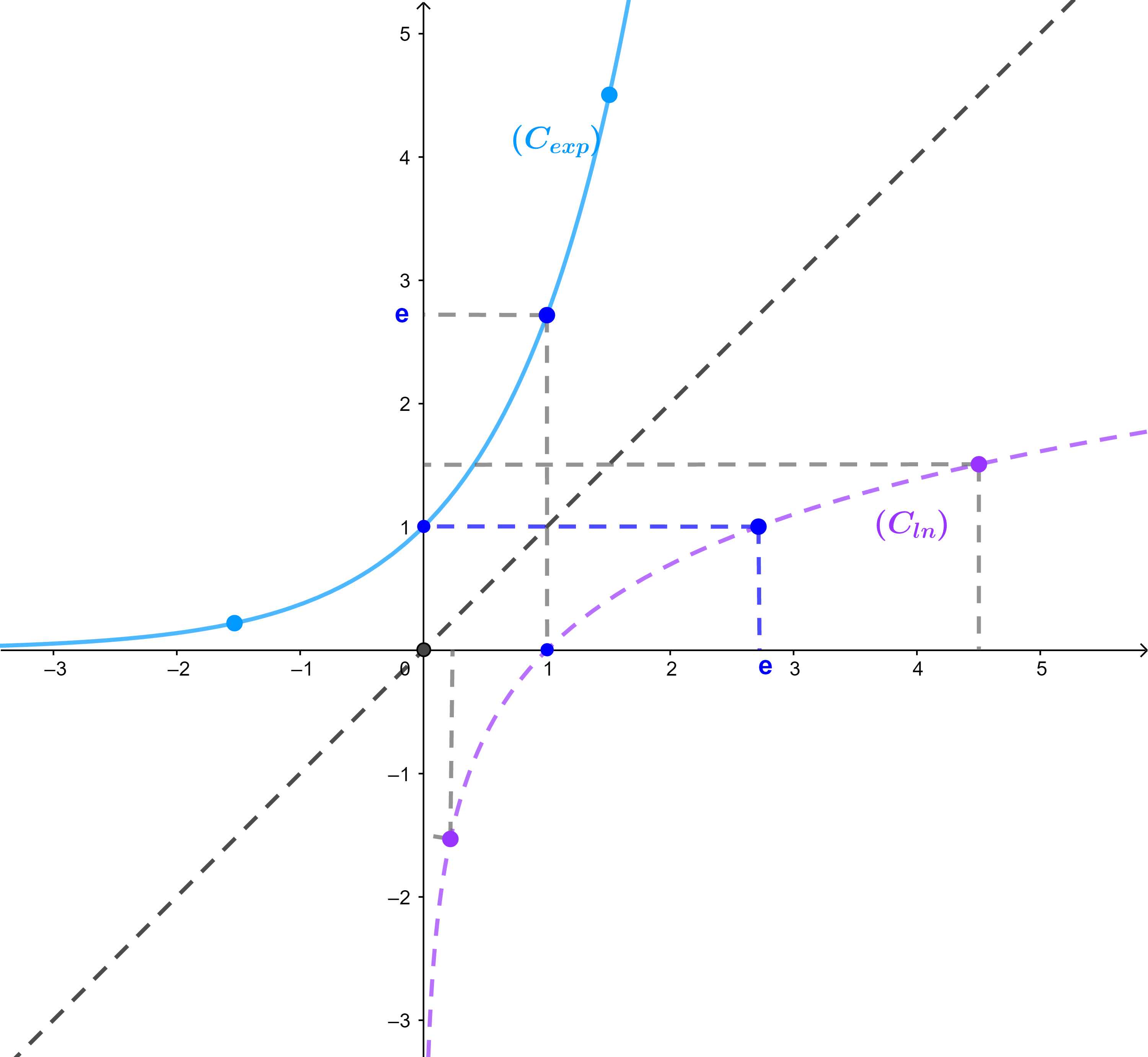
Le plan est rapporté à un repère orthonormé
(O;i→;j→) et (C) est la courbe représentative de la fonction exp tel que exp(x)=ex
1) Ensemble de définition D=IR
2) Limites et branches infinies
lim +∞ |
ex = +∞ | lim +∞ |
ex | = +∞ | |
| x |
On dit alors que la courbe (C) admet une branche parabolique de direction l'axe des ordonnées.
| On a | lim -∞ |
ex = 0 |
On dit alors que la courbe (C) admet l'axe des abscisses comme une asymptote.
3) Dérivée et monotonie
La fonction exp est dérivable sur IR
et pour tout x∈IR on a (ex)'=ex.
On sait que pour tout x∈IR on a ex>0 donc la fonction exp est strictement croissante sur IR.
Tableau de variations
| x | -∞ | +∞ | |
| f '(x) | + | ||
| f | 0 |
↗ |
+∞ |
4) On séléctionne des valeurs des abscisses convenables pour certains points de la courbe (C)
| x | -1 | 0 | 1 | 2 |
| ex | e-1≃-0,37 | 1 | e≃2,7 | e²≃7,9 |
Remarque La courbe de la fonction exp et la courbe de la fonction ln sont symétriques par rapport à la droit (D): y=x