Exercice 1 tp

Soit f une fonction définie par
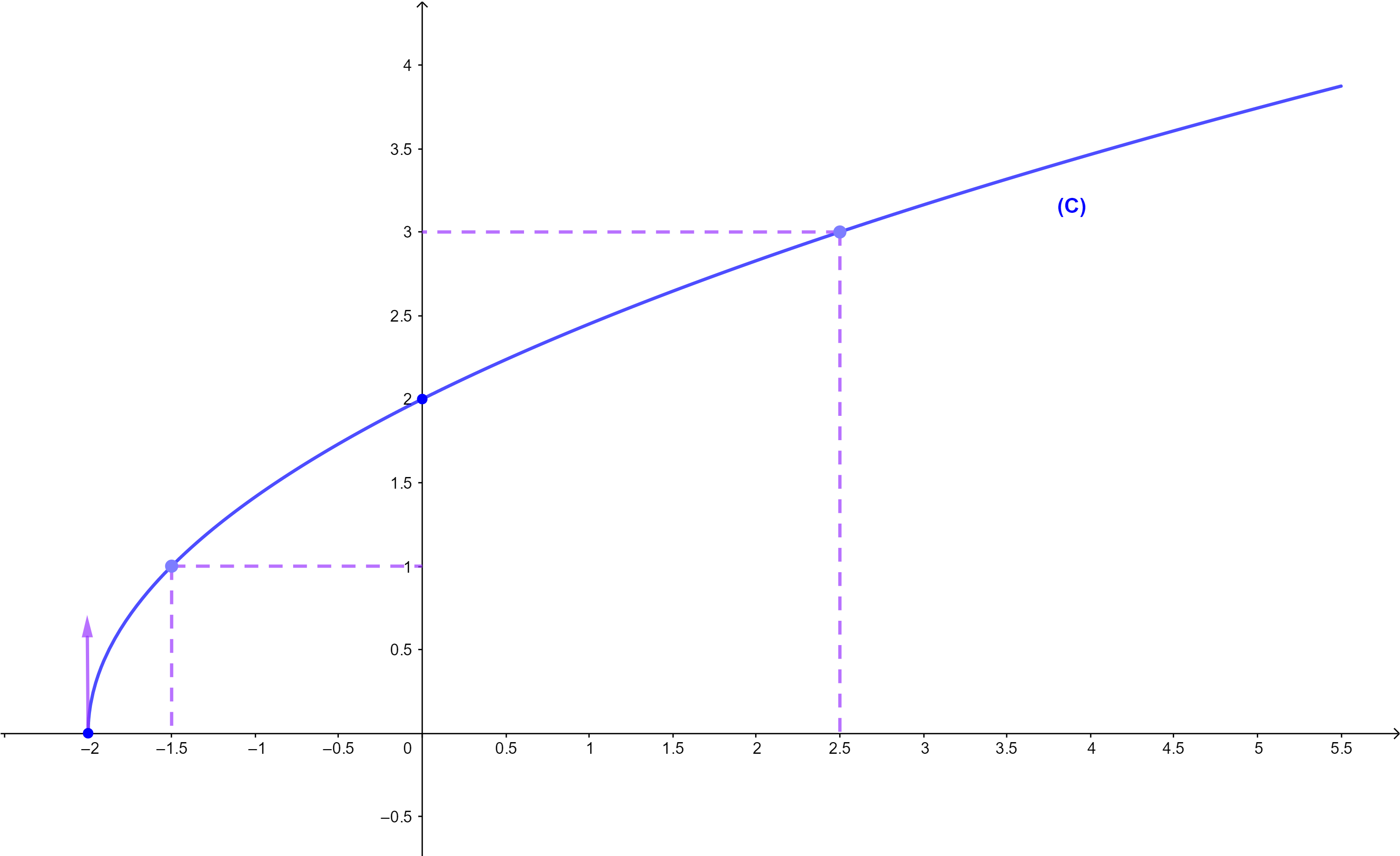
f(x)=√(4x+8) et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Déterminer l'ensemble de définition de f
2) Calculer

lim +∞

f(x)

3) Calculer f'(x) et étudier son signe sur D\{-2}.
4) En déduire la monotonie de f et tracer son tableau de variations.
5) Tracer la courbe (C)

Correction

1) f est définie signifie 4x+8≥0 signifie x≥-2
donc D=[-2;+∞[
2) Limite de f en +∞

lim +∞

4x + 8 =

lim +∞

4x = +∞

donc

lim +∞

f(x)

= +∞

3) f est dérivable si 4x+8>0 signifie x>-2
donc f est dérivable sur I=]-2;+∞[.

Soit x∈]-2;+∞[ calculons f'(x).

f'(x) =	(4x + 8)'
	2√(4x + 8)
=	4
	2√(4x + 8)

donc pour tout x∈I=]-2 ; +∞[

f '(x) =	2
	√(4x + 8)

4) Pour tout x∈I on a f '(x) > 0 car a=4>0
donc f est strictement croissante sur I

Tableau de variation de f

x	-2		+∞
f'(x)	||	+
f	0	↗	+∞

5) La courbe représentative de f

Exercice 1 tp

Soit f une fonction définie par
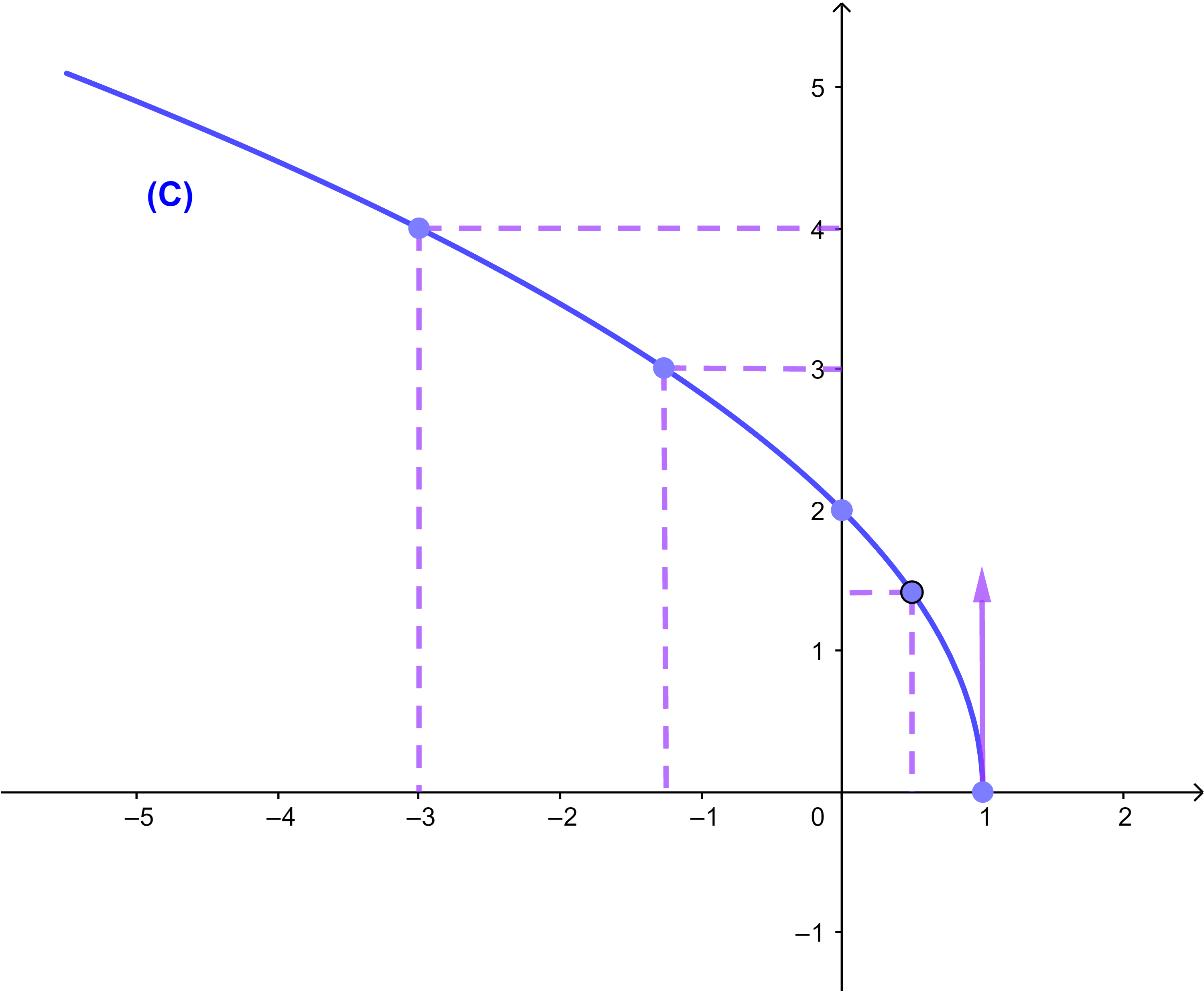
f(x)=√(-4x+4) et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Déterminer l'ensemble de définition de f
2) Calculer

lim -∞

f(x)

3) Calculer f'(x) et étudier son signe sur D\{1}.
4) En déduire la monotonie de f et tracer son tableau de variations.
5) Tracer la courbe (C)

Correction

1) f est définie si -4x+4≥0 signifie -4x≥-4
signifie 4x≤4 signifie x≤1 donc D=]-∞;1]
2) Limite de f en -∞

lim -∞

-4x + 4 =

lim -∞

-4x = +∞

donc

lim -∞

f(x)

= +∞

3) f est dérivable si -4x+4>0 signifie -4x>-4
signifie 4x < 4 signifie x < 1
donc f est dérivable sur I=]-∞;1[
Soit x∈]-∞;1[ calculons f'(x)

f'(x) =	(-4x + 4)'	=	-4
	2√(-4x + 4)		2√(-4x + 4)

donc pour tout x∈I=]-∞;1[

f '(x) =	-2
	√(-4x + 4)

4) Pour tout x∈I on a f '(x) < 0 car a=-4 < 0
donc f est strictement décroissante sur I

Tableau de variation de f

x	-∞		1
f'(x)		+	||
f	+∞	↘	0

5) La courbe représentative de f