تمرين 1 tp

1) لتكن f دالة عددية معرفة كما يلي
f(x) = -2x² + 4x + 1
و (C_f) منحناها في معلم متعامد ممنظم
(O ; i^→ ; j^→)
(a) احسب النهايتين التاليتين

lim - ∞

f(x)

lim + ∞

f(x)

(b) احسب f '(x) حيث x∈D
(c) ادرس رتابة الدالة f وانشئ جدول تغيراتها
(d) استنتج مطرافا للدالة f.

2) لتكن g دالة عددية معرفة كما يلي
g(x) = x² -4 x+ 5
a) احسب النهايتين التاليتين

lim - ∞

g(x)

lim + ∞

g(x)

(b) احسب f '(x) حيث x∈D
(c) ادرس رتابة الدالة f وانشئ جدول تغيراتها
(d) استنتج مطرافا للدالة f
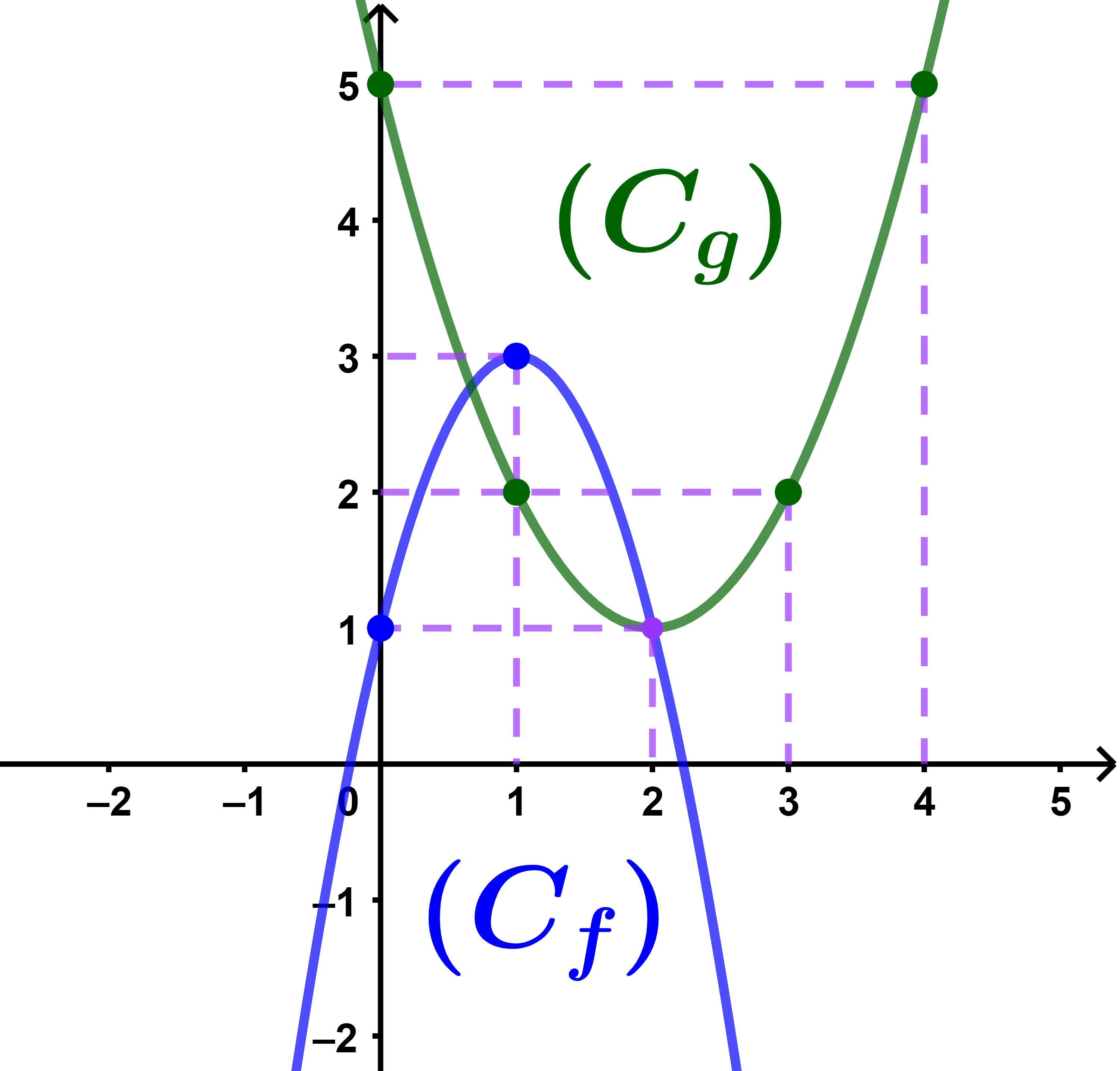
3) انشئ منحنى كل من الدالتين f و g في نفس المعلم وحل مبيانيا المعادلة f(x) = g(x).

تصحيح

1) (a) لدينا f حدودية اذن D = IR

lim - ∞	f(x)	=	lim - ∞	- 2x² = - ∞
lim + ∞	f(x)	=	lim + ∞	- 2x² = - ∞

(b) f دالة حدودية اذن قابلة للاشتقاق على IR. ليكن x∈IR
f'(x)=(-2x²+4x+1)'=-4x+4
اذن لكل (x∈IR) f'(x)=-4x+4
(c) اشارة f'(x)
f'(x)=0 ⇔ -4x+4=0 ⇔ 4x=4 ⇔ x=1

f'(x) تكتب على الشكل ax+b ولدينا a=-4<0

x		-∞		1		+∞
- 4x + 4			+	0	-

اذا كان x∈]-∞;1[ فان f'(x)>0
اذا كان x∈]1;+∞[ فان f'(x)<0
وبالتالي الدالة f تزايدية قطعا على ]-∞;1] وتناقصية قطعا على [1;+∞[
جدول التغيرات

x		-∞		1		+∞
f '(x)			+	0	-
f		-∞	↗	3	↘	-∞

(d) الدالة المشتقة f' تنعدم في 1 اي f'(1)=0
وتتغير اشارتها من (+) الى (-)
اذن الدالة f تقبل قيمة قصوى f(1)=3

2) (a) لدينا g حدودية اذن D_g=IR

lim - ∞	g(x)	=	lim - ∞	x² = + ∞
lim + ∞	g(x)	=	lim + ∞	x² = + ∞

(b) g دالة حدودية اذن قابلة للاشتقاق على IR. ليكن x∈IR
g'(x)=(x²-4x+5)'=2x-4.

(c) اشارة g'(x)
g'(x)=0 ⇔ 2x-4=0 ⇔ x=2
g'(x) تكتب على الشكل ax+b
ولدينا a=2>0

x		-∞		2		+∞
2x - 4			-	0	+

اذا كان x∈]-∞;2[ فان g'(x)<0
اذا كان x∈]2;+∞[ فان f'(x)>0
وبالتالي الدالة f تناقصية قطعا على ]-∞;2] وتزايدية قطعا على [2;+∞[.

x		-∞		2		+∞
g '(x)			-	0	+
g		+∞	↘	1	↗	+∞

(d) الدالة المشتقة g' تنعدم في 2 اي g'(2)=0
وتتغير اشارتها من (+) الى (-)
اذن الدالة g تقبل قيمة دنيا f(2)=1

3) المنحنيان (C_f) و (C_g) يتقاطعان في نقطتين اذن المعادلة f(x)=g(x) تقبل حلين أحدهما العدد 2 والآخر محصور بين 0 و 1.