(4) الدوال اللوغاريتمية
1.2 التمثيل المبياني للدالة ln
1) مجموعة التعريف الدالة ln
D=]0;+∞[.
2) النهايات نقبل النهايات التالية وتعتبر نهايات اعتيادية
(a) النهاية عند + ∞
lim +∞ |
ln(x) | = +∞ |
(b) النهاية عند 0+
lim 0+ | ln(x) | = - ∞ |
نتيجة 1 بما أن
lim 0+ |
ln(x) | = - ∞ |
نقول اذن أن المنحنى (C) يقبل مقاربا
معادلته x=0 (محور الأراتيب ).
(c) نهاية اعتيادية أخرى عند + ∞
lim +∞ |
ln(x) | = 0 |
| x |
نتيجة 2 بما أن
lim +∞ |
ln(x) | = 0 |
| x |
نقول اذن أن المنحنى (C) يقبل فرعا شلجميا في اتجاه محور الأفاصيل (Ox).
3) الاشتقاق والرتابة
الدالة ln قابلة الأشتقاق على ]0;+∞[.
ولدينا ∀x∈]0;+∞[
| (ln)'(x) = | 1 |
| x |
بما أن x>0 فان لكل
x∈]0;+∞[ لدينا ln'(x)>0
وهذا يعني ان الدالة ln تزايدية قطعا على ]0;+∞[.
| x | 0 | +∞ | ||
| f '(x) | || | + | ||
| f | || | -∞ |
↗ |
+ ∞ |
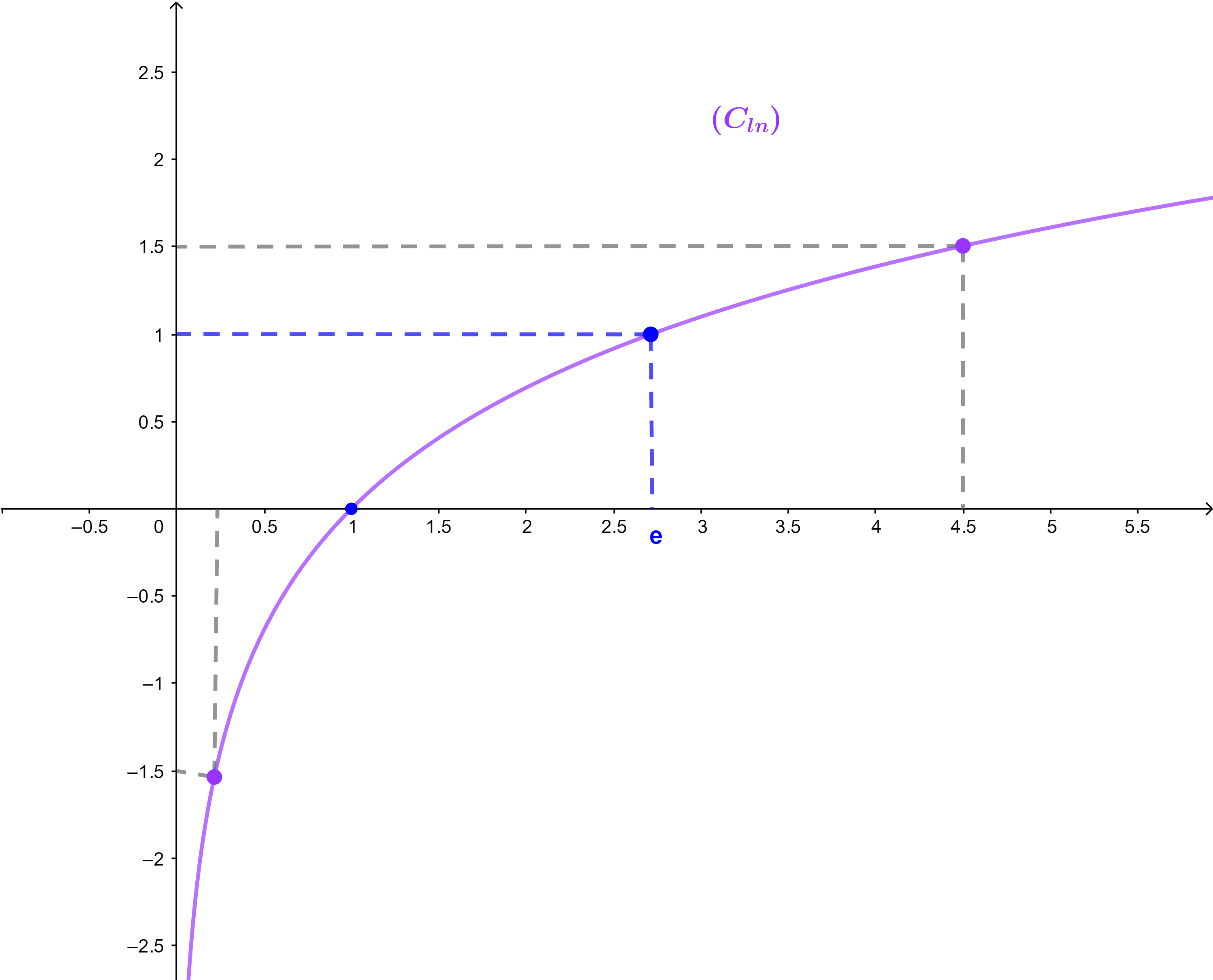
منحنى الدالة ln في معلم متعامد ممنظم (O;i→;j→).
تمرين 1 tp
احسب النهايات التالية
lim +∞ |
x²+ 1 + ln(x) |
lim +∞ |
lnx - (lnx)² |
lim 0+ |
lnx + (lnx)² |
تمرين 2 tp
احسب النهاية التالية
lim +∞ |
1 | + lnx |
| x |
تمرين 3 tp
احسب النهاية التالية
lim 0+ |
√(x) | + lnx |
| x |