حساب الاحتمالات (3)
1.2.5 الحدث المضاد والاحداث غير المنسجمة
الحدث المضاد
ليكن A و E حدثين من فضاء احتماليا منتهيا (Ω;p).
نقول ان A و E مضادان اذا كانا منفصلين اي A∩F=∅ وكان اتحادهما يساوي الحدث الاكيد أي A∪F=Ω.
بتعبير آخر
A و E مضادان ⇔ E∩A=∅ و E∪A=Ω.
ترميز نكتب A=Ē أو ايضا E=Ā.
بالاضافة الى ذلك p(A)=p(Ē)=1-p(E).
مثال
يحتوي صندوق على 7 كرات مرقمة كما يلي 0 ; 2 ; 4 ; 13 ; 14 ; 17 ; 18
0
2
4
13
14
17
18
نسحب كرة واحدة من الصندوق ونعتبر الحدث E: الرقم الذي يظهر يحمل رقما فرديا
13
17
لدينا cardΩ=7 و E={13;17} اذن cardE=2 ومنه فان احتمال الحدث E
| p(E) = | cardE | = | 2 |
| cardΩ | 7 |
احتمال الحدث المضاد للحدث E معرف كما يلي
| p(Ē) = 1 - p(E) = 1 - | 2 |
| 7 | |
| p(Ē) = | 5 | اذن |
| 7 | ||
ملاحظة Ē={0;2;4;14;18}.
الأحداث غير المنسجمة
حدثان E و F غير منسجمين يعني E∩F=∅.
ملاحظة
حدثان غير منسجمان لا يتحققان في وقت واحد.
مثال
عند رمي قطعة نقدية يظهر اما الوجه F واما الظهر P وليس كلاهما.
ملاحظة
حدثان مضادان هما حدثان غير منسجمان.
تمرين 1 tp
نرمي قطعة نقدية مرتين.
أحسب احتمالات كل من الأحداث التالية.
PP: ظهور الظهر مرتين.
FP: ظهور الوجه ثم الظهر.
E: ظهور الوجه مرة على الأقل.
تصحيح
مجموعة الامكانيات Ω={PP;PF;FP;FF}
اذن cardΩ=4.
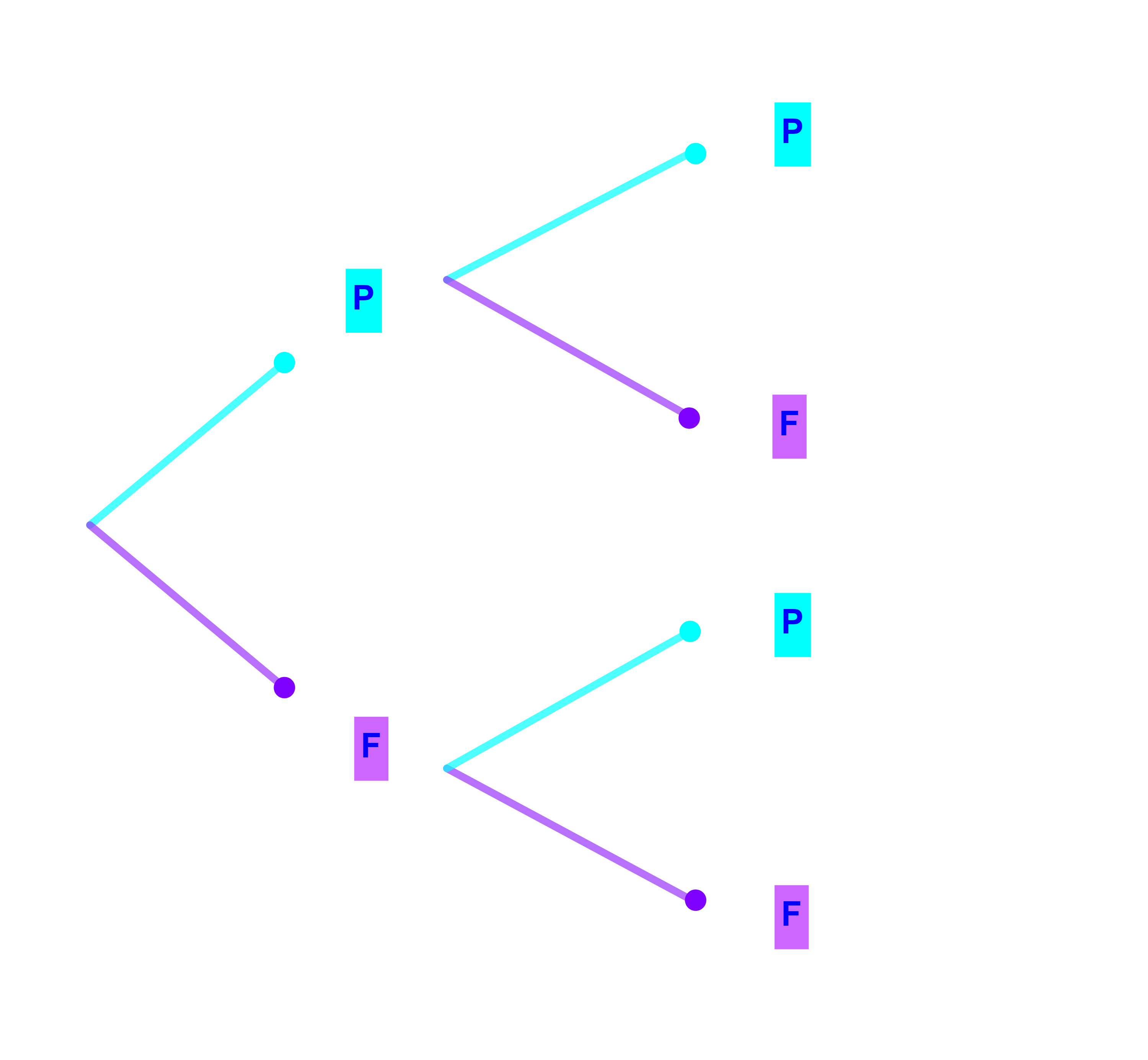
PP: ظهور الظهر مرتين
| p(PP) = | 1 |
| 4 | |
FP: ظهور الوجه ثم الظهر
| p(FP) = | 1 |
| 4 | |
E: هو الحدث E={FP;PF;FF}.
| p(E) = | 3 |
| 4 | |
ملاحظة
يمكن في هذه الحالة استعمال الحدث المضاد للحدث E
Ē: عدم ظهور الوجه أي Ē=PP
p(Ē)=p(PP)
ومنه فان p(E)=1-p(PP)
| p(E) = 1 - | 1 | = | 3 |
| 4 | 4 | ||