Les suites numériques (4)
2.2 Limite finie
2.2.1 Activité
Exemple 1
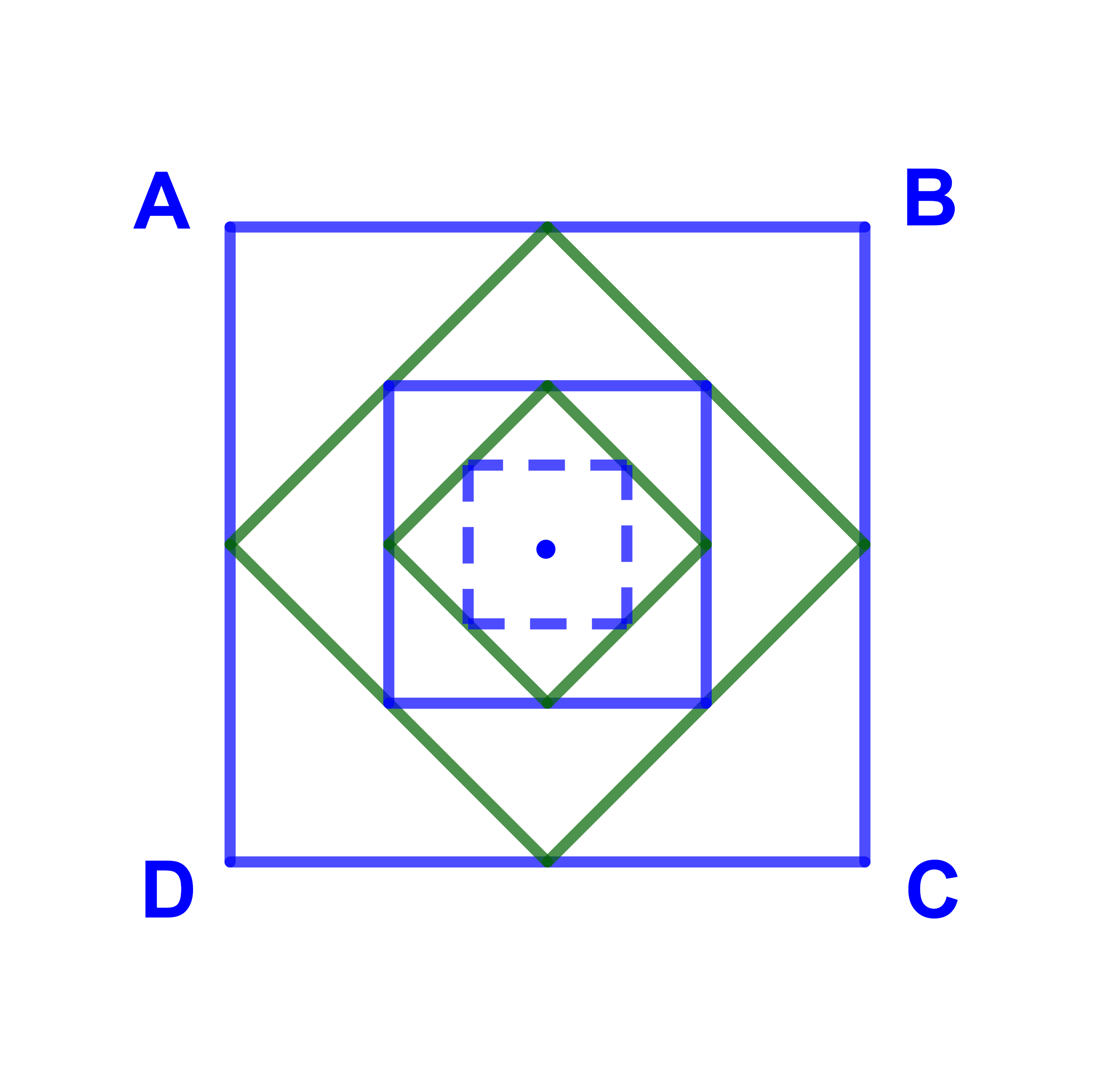
C0=(ABCD) est un carré de surface s0=1
C1 est un carré de surface s1 ses sommets sont les milieux des côtés du carré
C0 ...
Cnest un carré Sn ses sommets sonts les milieux des côtés du carré Cn-1
| Le carré | C0 | C1 | C2 | .. | Cn | ||||
| Indice | 0 | 1 | 2 | .. | n | ||||
| La surface | 1 | 1 | 1 | .. | 1 | ||||
| 4 | 4² | 4n-1 |
(Sn) est une suite géométrique de raison 1/4
Quand n prend une valeur grande le carré se rapproche d'être un point
donc sa surface se rapproche de 0.
On dit (limite de (Sn) est 0)
| et on écrit | lim +∞ |
(Sn) = 0 |
Exemple 2 Compléter le tableau suivant
| n | 10² | 10³ | 104 | ... | +∞ | |
| 1 | 0,01 | .. | .. | .. | 0 | |
| n | ||||||
| 1 | 0,0001 | .. | .. | 0 | ||
| n² | ||||||
| 1 | .. | .. | .. | .. | 0 | |
| n³ | ||||||
| 1 | 0,1 | .. | .. | .. | 0 | |
| √n |
Plus la valeur n est élévée, plus la valeur du terme général
de chacun de ces suites diminue et se rapproche de 0.
On dit que la limite de ces suites est 0 et sont considérées comme des suites de référence.
lim +∞ |
1 | = 0 | lim +∞ |
1 | = 0 | |
| n | n² | |||||
lim +∞ |
1 | = 0 | lim +∞ |
1 | = 0 | |
| n³ | √(n) |
lim +∞ |
1 | = 0 (p∈IN*) |
| np |
2.2.2 Définitions
1) Une suite (un) admet pour limite 0 si tout intervalle ouvert contenant 0, contient tous les termes de la suite à partir d'un certain rang et on écrit
lim +∞ |
(un)n∈I = 0 |
2) Si une suite (un)n∈I tend vers un nombre L
| on écrit | lim +∞ |
(un)n∈I = L |
2.2.3 Résultat
lim +∞ |
(un)n∈I = L ⇔ | lim +∞ |
(un)n∈I - L = 0 |
2.2.4 Définition
On dit qu'une suite est convergente si elle admet une limite finie.
Exemple Soit (un) une suite numérique définie par
| un = 7 + | 1 |
| n³ |
lim +∞ |
(un - 7) = | lim +∞ |
1 | = 0 |
| n³ |
| donc | lim +∞ |
(un) = 7 |