Le barycentre dans le plan (5)
3- associativité
3.1 Barycentre de 3 points
Soit G le barycentre des points pondérés (A;a) ; (B;b) et (C;c).
Si H est le barycentre de (A,a) ; (B;b) (a+b≠0)
alors G est le barycentre des points pondérés (H;a+b) et (C;c).
De même si K est le barycentre de (A;a) et (C;c) (a+c≠0)
alors G est le barycentre des points pondérés (K;a+c) et (B;b).
Ou encore si L est le barycentre de (B;b) et (C;c) (b+c≠0).
alors G est le barycentre des points pondérés (L;b+c) et (A;a).
3.1.1 Propriété
Le barycente de trois points ne change pas si on remplace deux points par leur barycentre s'il existe.
Exercice 1 tp
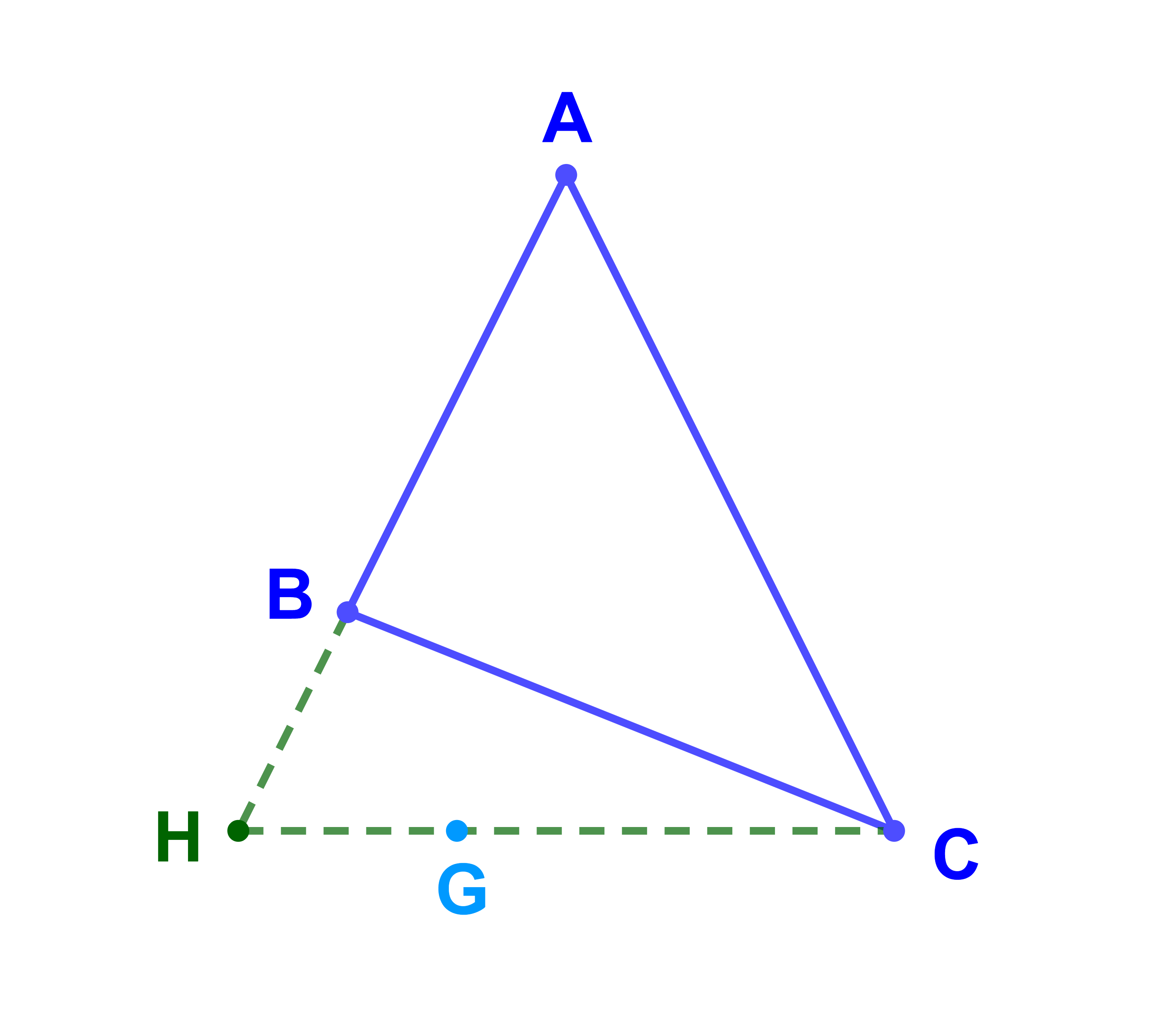
Tracer G le barycentre des points pondérés (A;-1) ; (B;3) et (C;1).
Correction
Les deux points pondérés (A,-1) et (C,1) n'ont pas de barycentre
car -1+1=0 donc on ne peut pas appliquer la propriété d'association aux points A et C.
Les points pondérés (A;-1) et (B;3) admettent un barycentre noté H car -1+3=2≠0.
Donc G est le barycentre des points pondérés (H;2) et (C;1).
Remarque 1 on peut appliquer également la propriété d'association aux points B et C car 3+1=4≠0.
Remarque 2 pour tracer le point G il suffit de tracer les points H et C.
H est le barycentre de (A;-1) ; (b;3) ⇔
(∀M): -MA→+3MB→=(-1+3)MH→
⇔
(∀M): -MA→+3MB→=2MH→.
On pose M=B
donc -BA→=2BH→
⇔
| BH→ = - | 1 | BA→ |
| 2 |
On a
(∀M): -MA→+3MB→+MC→=3MG→
⇔
2MH→+MC→=3MG→
on pose M=H donc
HC→=3HG→
ainsi
| HG→ = | 1 | HC→ |
| 3 |