Exercice 1 tp

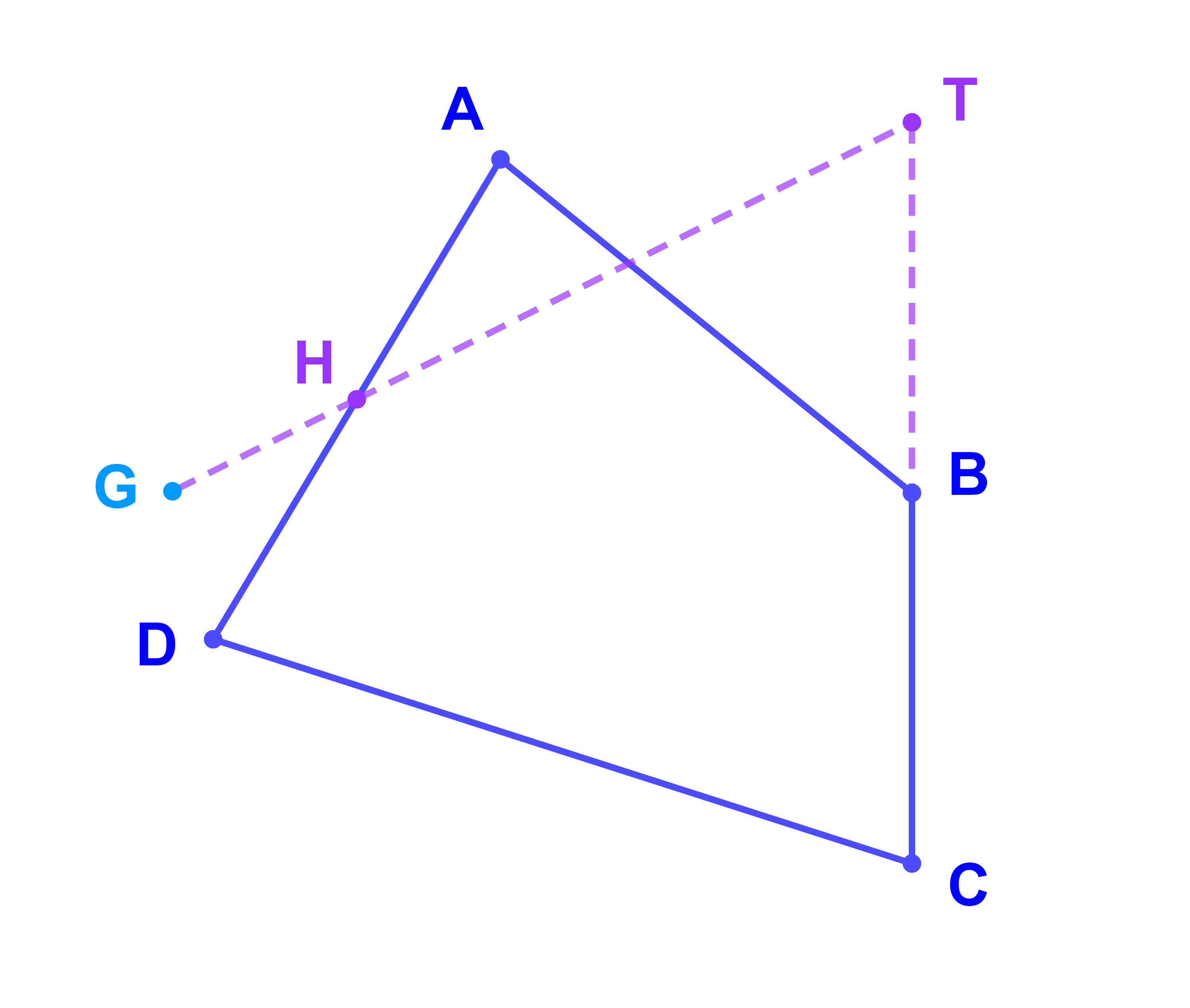
Construire G le barycentre des points pondérés (A;2) ; (B;-2) ; (C;1) et (D;2).

Correction

(A,2) ; (B,-2) n'admettent pas de barycentre car 2+(-2)=0 donc l'assocaition ne pas être appliquée sur A et B.
Les deux points (A;2) et (D;2) admettent un barycentre H car 2+2=4≠0 ainsi G est le barycentre des points pondérés (H;4) ; (B;-2) ; (C;1).

On applique l'association sur B ; C car -2+1=-1≠0 et ils admettent un barycentre T
ainsi G est le barycentre des points pondérés (H;4) et (T;-1).
Il suffit donc de tracer H et T pour tracer G.
On a H est le barycentre de (A;2) et (D;2) donc pour tout M
2MA^→+2MD^→=4MH^→
⇔ MA^→+MD^→=2MH^→
et cela signifie que H est le milieu du segment [AD].

T est le barycentre de (B;-2) ; (C;1)
Donc pour tout point M du plan
-2MB^→+MC^→=-MT^→
⇔ BT^→=-BC^→
on sait que pour tout M
2MA^→+2MD^→-2MB^→+MC^→=3MG^→
⇔ 4MH^→-MT^→=3MG^→
⇔ -HT^→=3HG^→ alors