Le barycentre dans le plan (4)
Exercice 1 tp
Soient G le barycentre des points pondérés (A;-3) ; (B;1) ; (C;1)
et E un point tel que AB→=-2AE→.
On considère F le projeté de E sur (AC) selon la direction (BC).
1) Montrer
| AF→ = | 1 | AC→ |
| 2 |
2) Montrer que G appartient à la droite passant par A et par I, le milieu du segment [BC].
3) Montrer que IG→=3IA→.
4) Montrer que les droites (CE); (BF) ; (AI) se coupent en G.
Correction
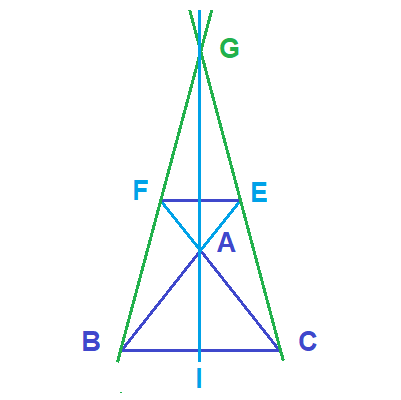
1) Notons que la projection concerve le coefficent de colinéarité de deux vecteurs.
On a AB→=-2AE→
et A; C; F les projetés respectifs de A; B; E sur (AC) selon la direction (BC)
donc
| AC→=-2AF→⇔ AF→ = - | 1 | AC→ |
| 2 |
2) G est le barycentre de (A;-3) ; (B;1) ; (C;1) et 1+1=2≠0 alors (B;1) et (C;1) admettent un centre de gravité, noté I ainsi G est le barycentre des points pondérés (A;-3) ; (I;2) et donc G∈(AI).
3) On montre que IG→=3IA→.
G est le barycentre de (A;-3) et (I;2) donc
-3GA→+2GI→
=O→ ⇔-3GI→-3IA→+2GI→=O
⇔ -GI→=+3IA→
⇔ IG→=3IA→.
4) On a AB→=-2AE→
⇔ GB→-GA→=-2(GE→-GA→)
⇔ GB→-3GA→=-2GE→
⇔ -GC→=-2GE→
⇔ GC→=2GE→
donc G∈(CE).
de la même façon on montre que G∈(BF)
donc G∈(AI)∩(CE)∩(BF).