Dérivation (11)
3.2 Extremum d’une fonction
3.2.1 Propriété 1
Soient f une fonction dérivable sur I et a∈I.
Si f admet un extremum au point a alors f'(a)=0.
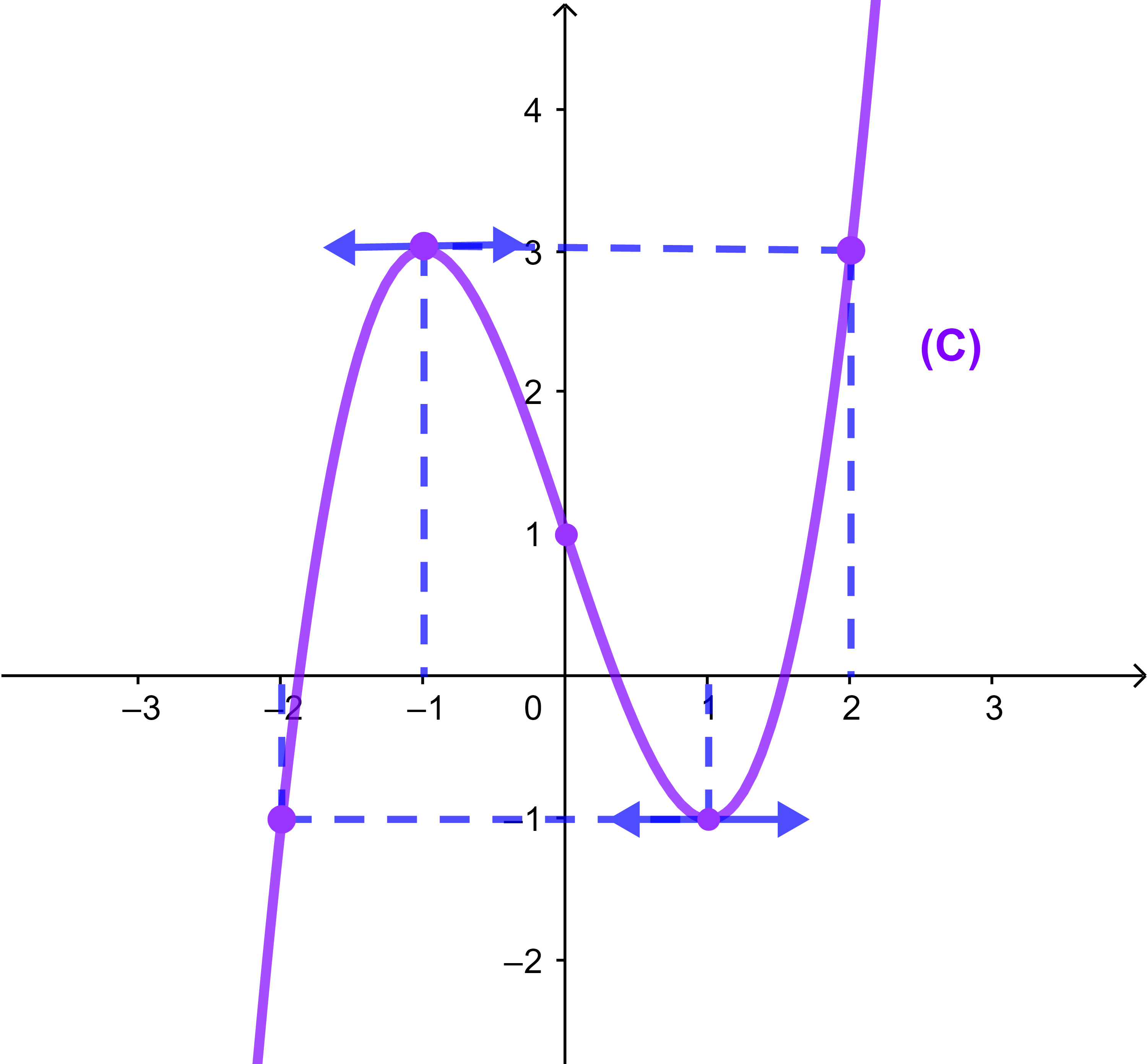
Remarque
La réciproque n'est pas toujours vraie
On prend un contre exemple si f(x)=x³ alors f'(0)=0 mais f n'admet pas d'extrmum au point 0.
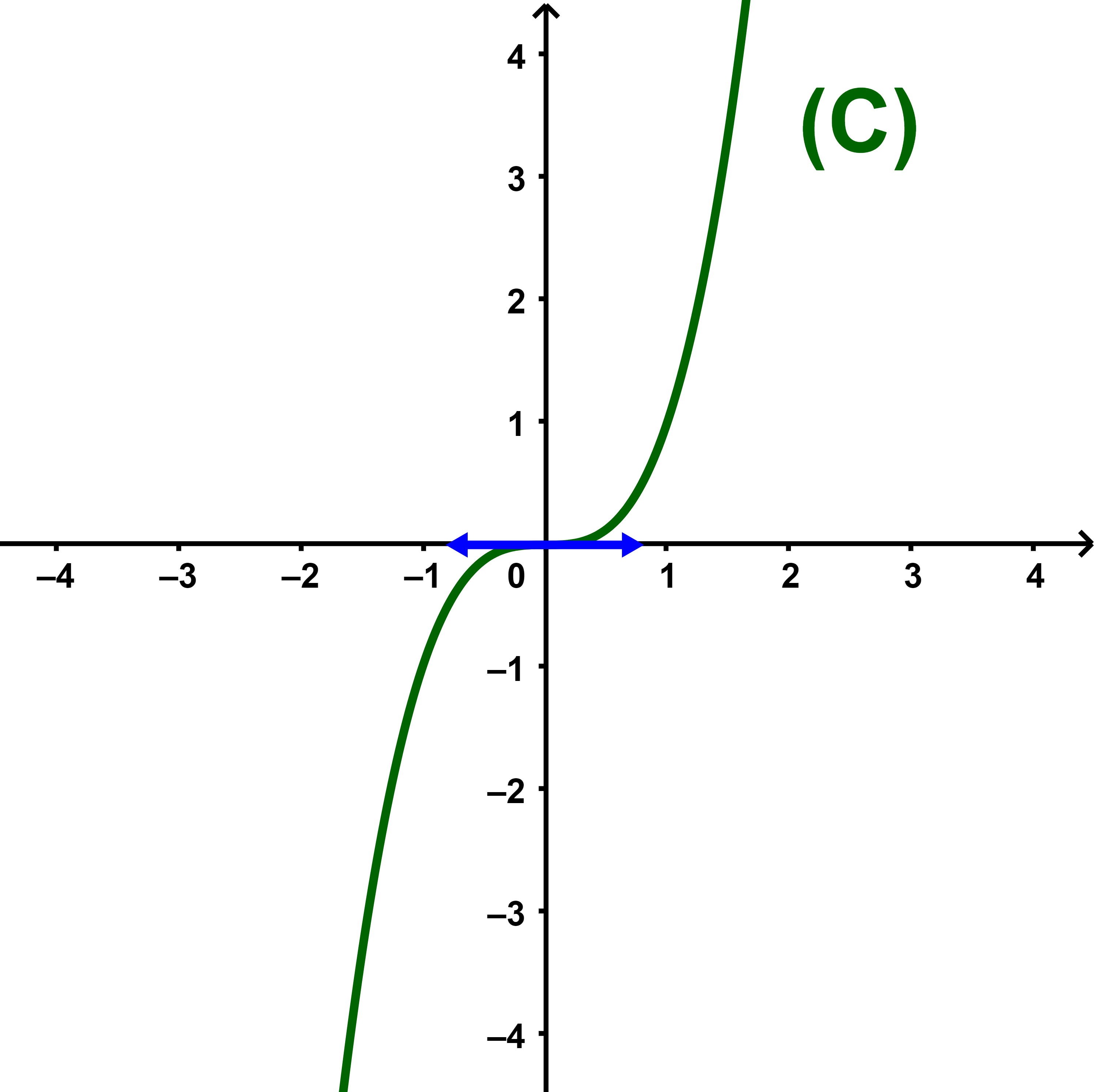
3.2.2 Propriété 2
Soient f une fonction dérivable sur I et a∈I.
Si f' s'annule au point a et change de signe en a
alors f(a) est un exremum de f.
Exemple
Soit f une fonction définie par f(x)=x³-3x.
Etudier la monotonie de f et déduire les extremums de f.
Correction
f est un polynôme donc f est dérivable sur IR. Soit x∈IR
f'(x)=3(x²-1)
donc f'(x)=0 ⇔ (x=1 ou x=-1).
Signe de f'
| x | -∞ | -1 | 1 | +∞ | |||
| f' | + | 0 | - | 0 | + |
f est strictement croissante sur ]-∞;-1] et strictement croissante sur [1;+∞[ et strictement décroissante sur [-1;1].
Tableau de variations
| x | -∞ | -1 | 1 | +∞ | |||
| f' | + | 0 | - | 0 | + | ||
| f | -∞ |
↗ |
2 | ↘ |
-2 |
↗ |
+∞ |
Remarque
f' s'annule au point -1 et change de signe de (+) à (-)
donc f(-1)=2 est une valeur maximale dans ]-∞;1[.
f' s'annule au point 1 et change de signe de (-) à (+)
donc f(1)=-2 est une valeur minimale dans ]-1;+∞[.