Exercice 1 tp

Soient f une application définie de E vers F ; A et B deux parties de E.
1) (a) Montrer que f(A∩B)⊂f(A)∩f(B).
(b) On suppose que f est injective.
est ce que f(A∩B)=f(A)∩f(B) ?
2) Montrer que f(A)∪f(B)=f(A∪B).

Correction

1) (a) on montre que f(A∩B)⊂f(A)∩f(B)
on a (A∩B) ⊂ A ⇒ f(A∩B) ⊂f(A)
et (A∩B) ⊂ B ⇒ f(A∩B) ⊂f(B)
donc f(A∩B)⊂f(A)∩f(B).

(b) d'après ce qui précède, f(A∩B)⊂f(A)∩f(B).
On montre donc f(A)∩f(B)⊂f(A∩B)
on a y∈f(A)∩f(B) ⇒ y∈f(A) ∧ y∈f(B)
⇒ (∃x1∈A: f(x1)=y) ∧ (∃x2∈B: f(x2)=y)
puisque f est injective alors y=f(x1)=f(x2) ⇒ x1=x2=x
donc (∃x∈A∩B)/ f(x)=y et cela signifie que y∈f(A∩B)
ainsi si f est injective alors f(A∩B)=f(A)∩f(B).
2) On montre que f(A)∪f(B)=f(A∪B) Notons que I=J ⇔((I⊂J) ∧ (J⊂I)).

On a A⊂A∪B ⇒ f(A)⊂f(A∪B)
et B⊂A∪B ⇒ f(B)⊂f(A∪B)
donc f(A)∪f(B)⊂f(A∪B).
On montre que f(A∪B)⊂f(A)∪f(B)
on a y∈f(A∪B) ⇔ (∃x∈A∪B/ f(x)=y)
et x∈A∪B ⇔ x∈A ∨ x∈B
donc ∃x∈A/ f(x)=y ∨ ∃x∈B/ f(x)=y
et cela signifie que y∈f(A) ∨ y∈f(B)
ou encore y∈f(A)∪f(B) ou encore f(A∪B)⊂f(A)∪f(B)
alors f(A∪B) = f(A)∪f(B).

Exercice 2 tp

Soit f une application définie de E vers F.
1) Montrer que si f est strictement monotone sur E alors elle set injective.
2) Montrer par un contre exemple que la réciproque est fausse.

Correction

1) On suppose que f est strictement monotone sur E c'est à dire elle est strictement croissante sur E ou bien strictement décroissante sur E.

Soit f strictement décroissante sur E
on montre que E est injective (de la même façon si on considère que f est strictement croissante sur E)
Notons que f est injective dans E signifie que
∀(x;y)∈E²: f(x)=f(y) ⇒ x=y
donc on montre que ∀(x;y)∈E²:
f(x)=f(y) ⇒ x=y.
Ou bien on utilise le raisonnement par contraposé
∀(x;y)∈E²: x≠y ⇒ f(x)≠f(y)

x≠y ⇒x<y ∨ x>y
soit x<y (de la même façon si on considère que x>y)
x<y ⇒ f(x)>f(y) car f est strictement décroissante
f(x)>f(y) ⇒ f(x)≠f(y)
donc (∀(x;y)∈E²): x≠y ⇒ f(x)≠f(y)
et cela signifie que f est injective sur E.
2) La réciproque est fausse contre exemple
E={-2;-1;5} et F={1;4;10;25}.

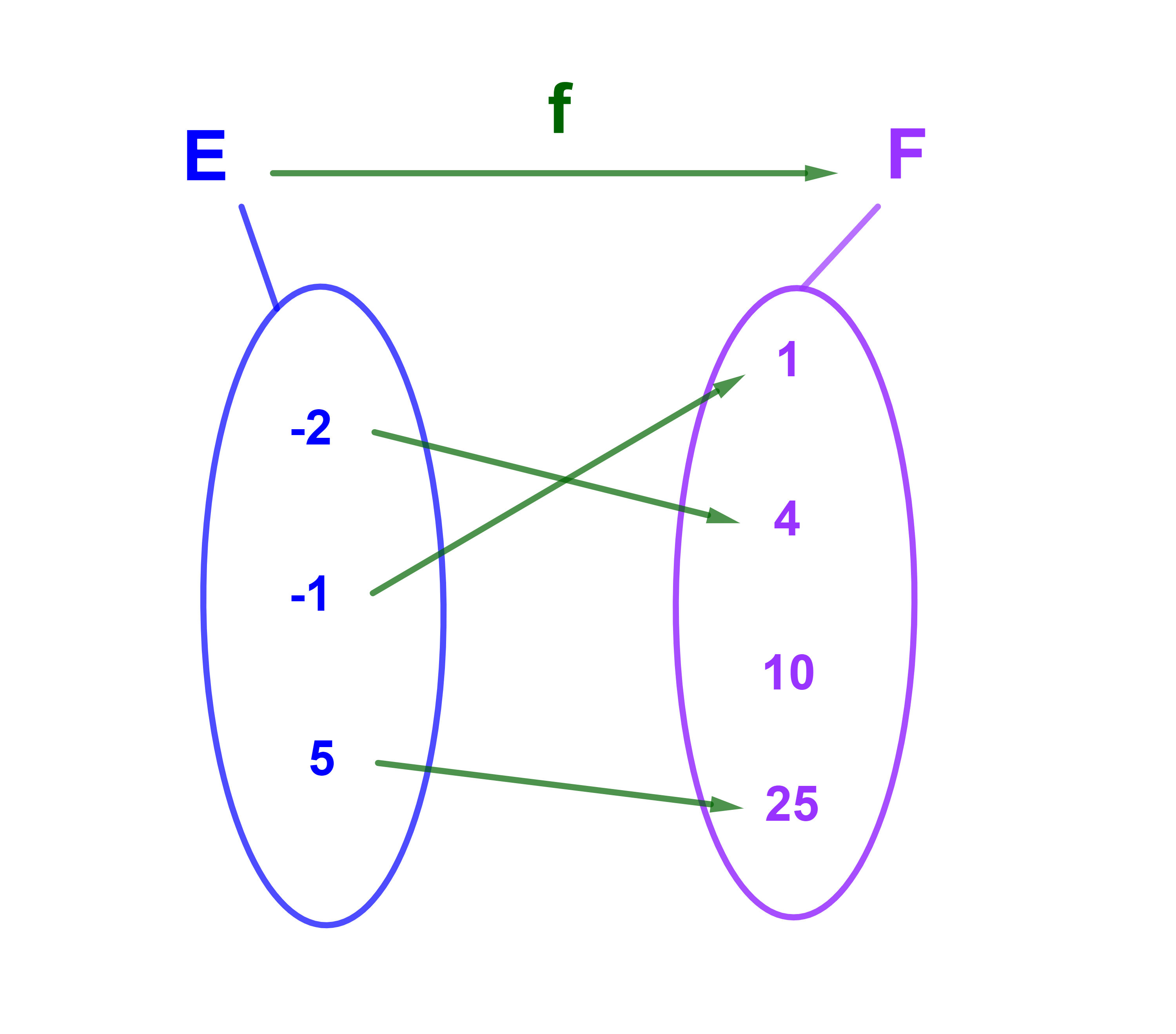
f est une application injective
on a
-2<-1 et f(-2) > f(-1)
et on a
-1<5 et f(-1) < f(5)
donc f n'est pas monotone sur E.