Etude des fonctions numériques (2)
Exercice 1 tp
Soit f une fonction définie par
| f(x) = x-1+ | 1 |
| x-1 |
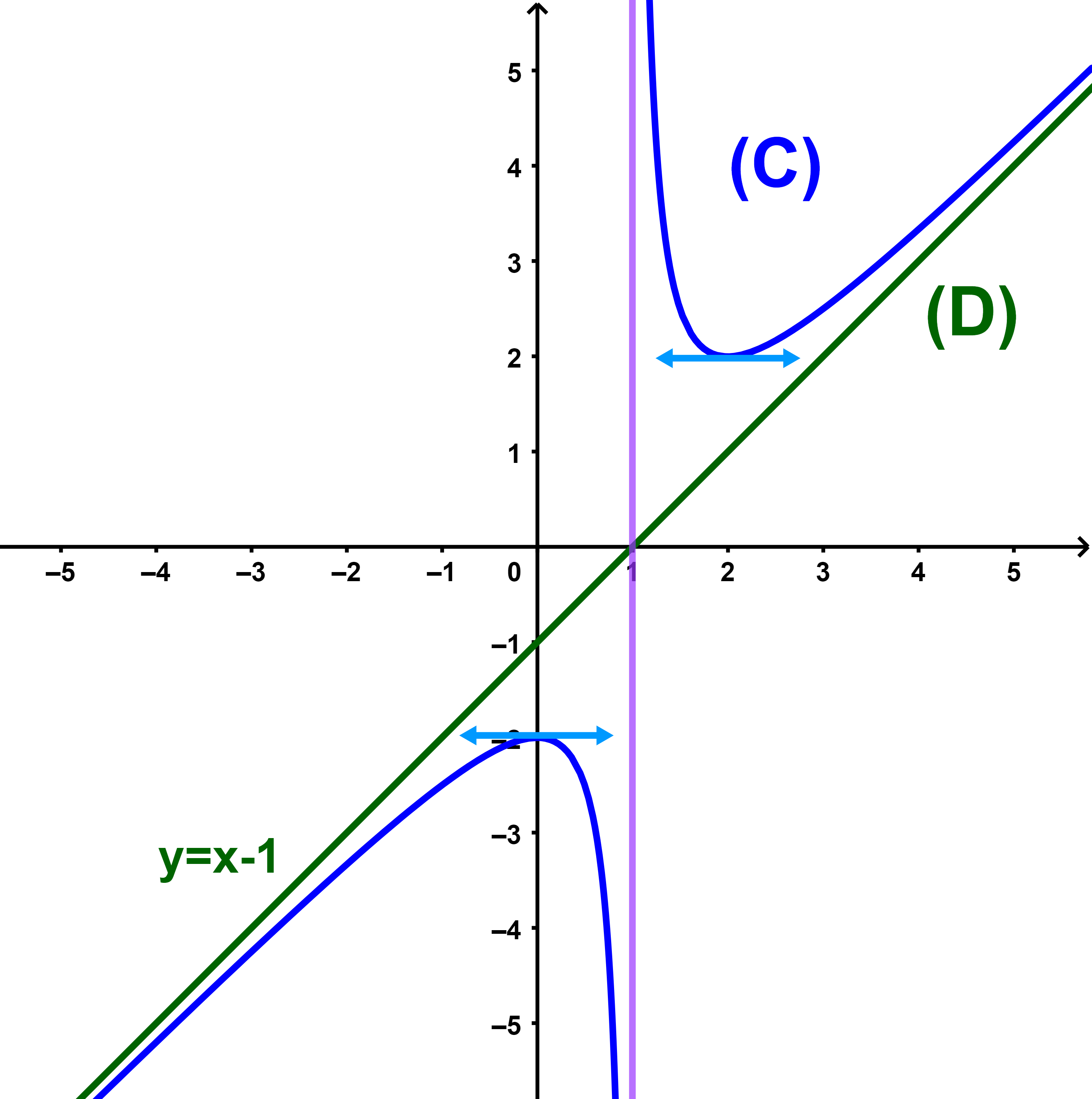
et (C) sa courbe représentative dansun repère orthonormé (O ;i→;j→).
Déterminer une asymptote oblique à (C).
Correction
D'abord on vérifie que f admet une limite infinie en +∞ ou en -∞.
On a
lim +∞ |
x-1 = | lim +∞ |
x = +∞ |
| et | lim +∞ |
1 | = | lim +∞ |
1 | = 0 |
| x-1 | x |
| donc | lim +∞ |
f(x) = +∞ |
Maintenant on calcule la limite de f(x)-(x-1).
lim +∞ |
f(x)-(x-1) = | lim +∞ |
1 | = 0 |
| x-1 |
| donc | lim +∞ | f(x)-(x-1)= 0 |
ainsi la droite (D):y=x-1 est une asymptote oblique à (C) au voisinage de +∞.
On fait le même travail quand x tend vers -∞
| on obtient | lim -∞ |
f(x)-(x-1) = 0 |
ainsi la même droite (D):y=x-1 est une asymptote oblique à (C) au voisinage de -∞.
Propriété 2
Soit f une fonction qui admet une limite infinie en +∞ ou -∞ et (C) sa courbe représentative dans un repère orthonormé (O ;i→;j→).
| Si | lim ±∞ | f(x) | = a et | lim ±∞ | f(x)-ax = b |
| x |
alors la droite d'équation y=ax+b est une asymptote oblique à la courbe (C) au voisinage de +∞ ou -∞.
1.2 Direction asymptotique
1.2.1 Branche parabolique de direction l'axe des abscisses
Soit f une fonction qui admet une limite infinie en ±∞ et (C) sa courbe dans un repère orthonormé (O ;i→;j→).
| Si | lim ±∞ | f(x) | = 0 |
| x |
Exemple
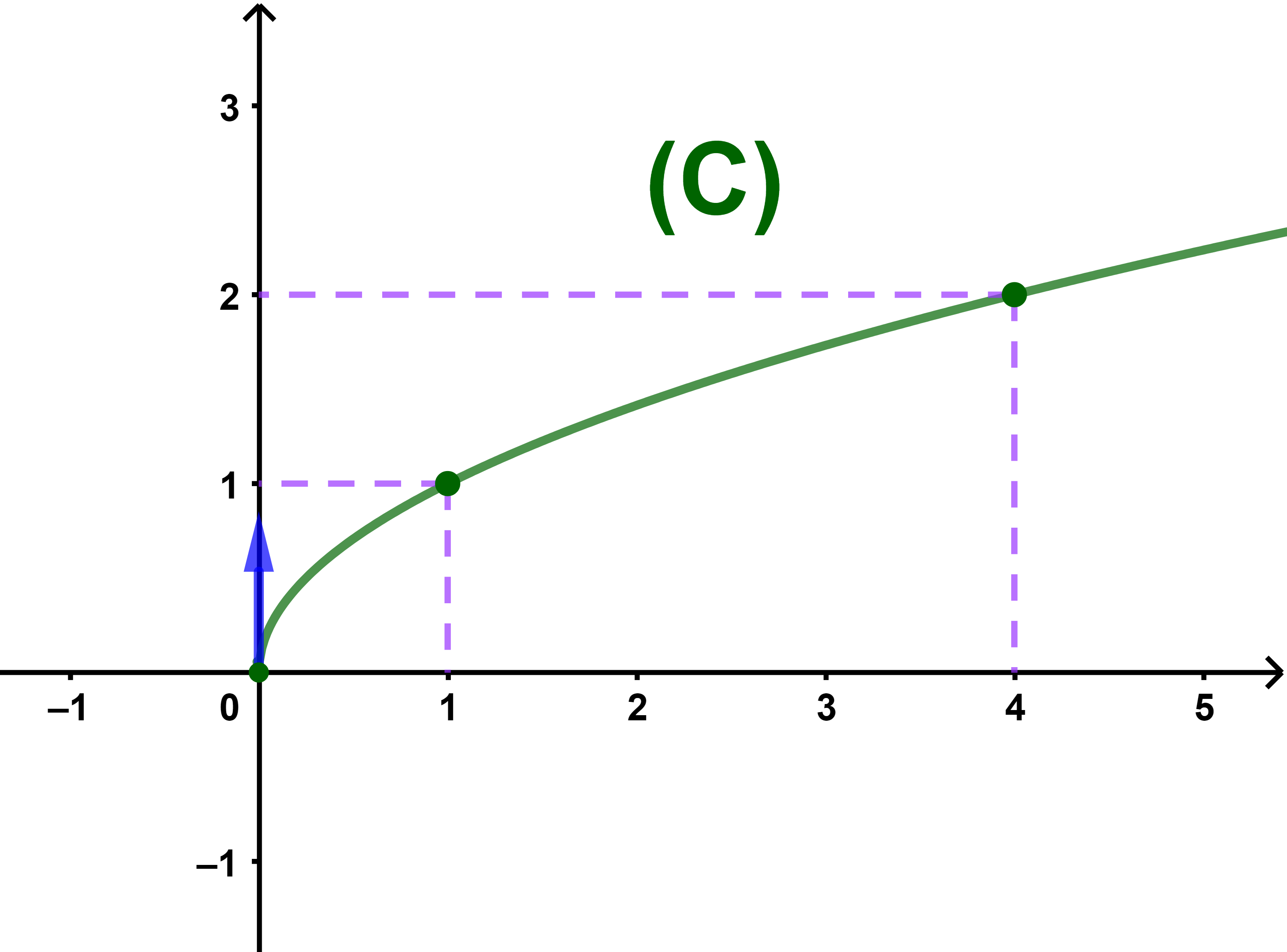
Soit f une fonction définie par f(x)=√x et (C) sa courbe dans un repère orthonormé (O ;i→;j→).
| 1) | lim +∞ |
f(x) = | lim +∞ |
√x = +∞ |
| 2) | lim +∞ |
f(x) | = | lim +∞ |
1 | = 0 |
| x | √(x) |
et donc (C) admet une branche parabolique de direction l'axe des abscisses (Ox).