3- القوانين المنطقية والاستدلالات

3.1 القوانين المنطقية

3.1.1 خاصيات

لتكن p و q و r عبارات منطقية.

p	⇔	⌉(⌉p)
⌉(p∧q)	⇔	(⌉p) ∨(⌉q)
(p∧q)	⇔	(q∧p)
(p∨q)	⇔	(q∨p)
⌉(p∨q)	⇔	(⌉p)∧(⌉q)

قانون مورغان
p∧(q∨r)	⇔	(p∧q)∨(p∧r)
p∨(q∧r)	⇔	(p∨q)∧(p∨r)

الاستلزام المضاد للعكس
(p⇒q)	⇔	(⌉q⇒ ⌉p)

مثال حدد مجموعة تعريف الدالة f المعرفة كما يلي

f(x) =	1
	x²-2x+1

المضاد للعكس (f معرفة اذا كان x²-2x+1≠0)
هو (f غير معرفة اذا كانت x²-2x+1=0).

x²-2x+1=0⇔(x-1)²=0⇔x-1=0⇔x=1.
نستنتج اذن أن f معرفة اذا كان x≠1
ومنه فان D=IR\{1}.

⌉(∀x/ p(x))	⇔	∃x/ ⌉p(x)
⌉(∃x/ p(x))	⇔	∀x/ ⌉p(x)
⌉(∃x ∀y)/ p(x ; y))	⇔	∀x ∃y/ ⌉p(x ; y))

3.1.2 مثال

حل النظمة التالية

{	x²-4 =	0
	y =	3

تصحيح
نستعمل قانون مورغان
((x²-4=0)∧y=3) ⇔([(x-2)(x+2)=0]∧y=3)
⇔ [(x=2∨x=-2)]∧y=3
⇔(x=2∧y=3)∨(x=-2∧y=3)
وبالتالي S={(2;3) ; (-2;3)}.

تمرين 3 tp

حل النظمة التالية

{	x²-4 =	0
	(y-1)(y+3) =	0

3.2 الاستدلالات المنطقية

للتذكير

1) عبارة منطقية تكون اما صحيحة واما خاطئة.
2) عبارة منطقية لا يمكن ان تكون صحيحة وخاطئة في آن واحد.
3) اذا كانت عبارة صحيحة و الاستلزام صحيحا فان العبارة صحيحة ايضا عمليا للبرهنة على صحة الاستلزام p⇒q يكفي ان ان نفترض ان العبارة p صحيحة ونبين ان العبارة صحيحية ايضا .

3.2.1 الاستدلال بالخلف

للبرهنة على صحة عبارة q يكفي اتباع المراحل التالية
1) نفترض ان هذه العبارة خاطئة .
وانطلاقا من هذا الافتراض نصل الى ان هذه العبارة ونفيها ⌉q صحيحتين معا وهذا غير ممكن.
2) وبالتالي نستنتج ان الافتراض كان خاطئا اي ان العبارة صحيحة.

مثال
ليكن ABC مثلثا بحيث AB=5,4 و BD=3 و CE=2,25 و AC=4,25 و E∈[AC] و D∈[AB]
هل (DE)||(BC) ?

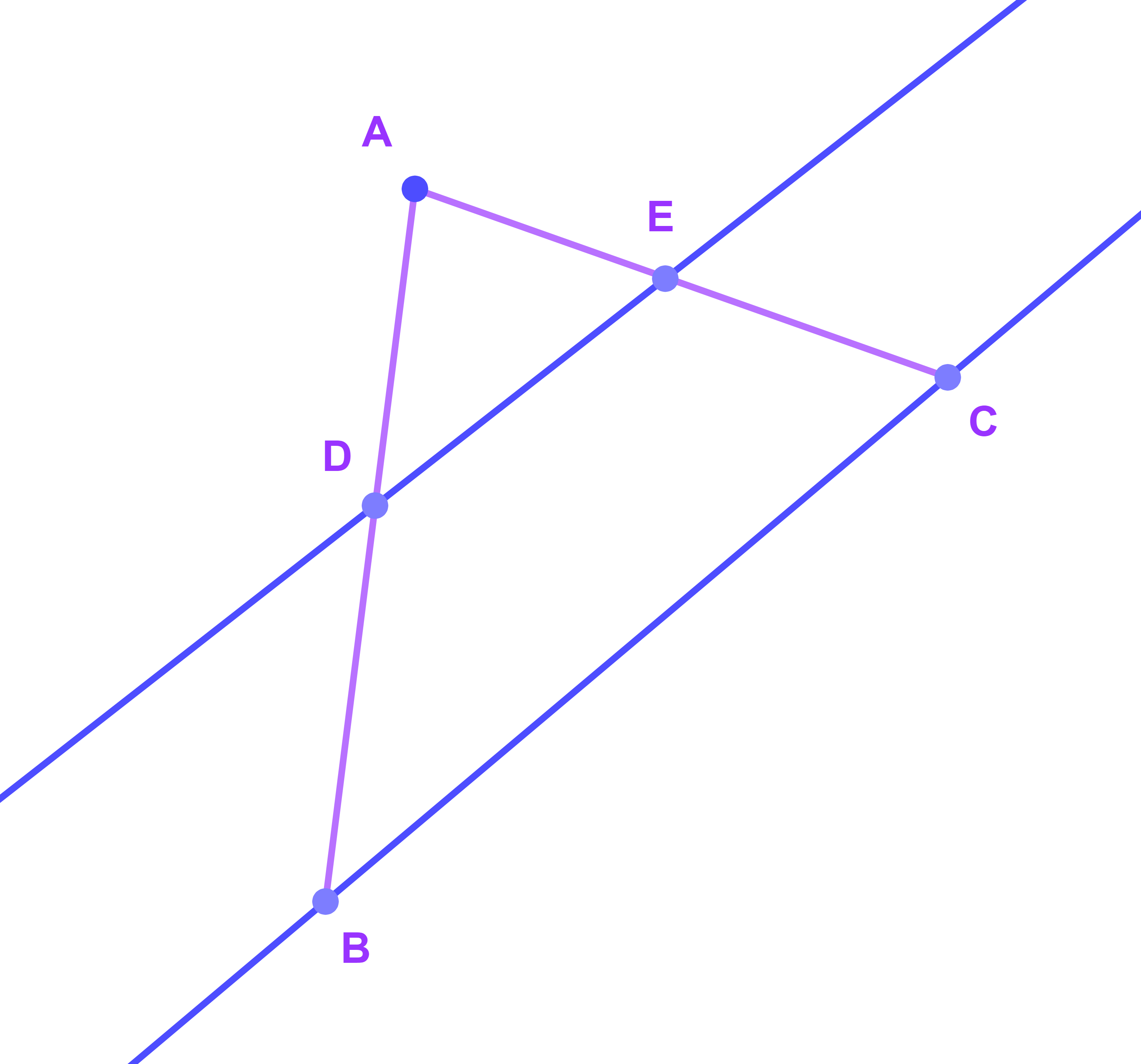
تصحيح

نفترض ان المستقيمين متوازيان (DE)||(BC).
حسب مبرهنة طاليس ان

AB	=	AC
BD		CE
5,4	=	5,25
3		2,25

5,4.2,25=3.4,25 اي 12,15=12,75 وهذا غير ممكن
نستنتج اذن ان المستقيمين (DE) و (BC) غير متوازيين.