3- Lois logiques et raisonnements

3.1 Lois logiques

3.1.1 Propriétés

Soient p ; q et r trois propositions.

p	⇔	⌉(⌉p)
⌉(p∧q)	⇔	(⌉p) ∨(⌉q)
(p∧q)	⇔	(q∧p)
(p∨q)	⇔	(q∨p)
⌉(p∨q)	⇔	(⌉p)∧(⌉q)

Loi de Morgan
p∧(q∨r)	⇔	(p∧q)∨(p∧r)
p∨(q∧r)	⇔	(p∨q)∧(p∨r)

Impliquation contraposée
(p⇒q)	⇔	(⌉q⇒ ⌉p)

Exemple Déterminons l'ensemble de définition de la fonction f définie par

f(x) =	1
	x²-2x+1

La contraposée de (f est définie si x²-2x+1≠0)
est (f n'est pas définie si x²-2x+1=0).

x²-2x+1=0⇔(x-1)²=0⇔x-1=0⇔x=1.
On déduit donc que f est définie si x≠1 ainsi D=IR\{1}.

⌉(∀x/ p(x))	⇔	∃x/ ⌉p(x)
⌉(∃x/ p(x))	⇔	∀x/ ⌉p(x)
⌉(∃x ∀y)/ p(x ; y))	⇔	∀x ∃y/ ⌉p(x ; y))

3.1.2 Exemple

Résoudre le système suivant

{	x²-4 =	0
	y =	3

Correction
On utilise la loi de Morgan
((x²-4=0)∧y=3) ⇔([(x-2)(x+2)=0]∧y=3)
⇔ [(x=2∨x=-2)]∧y=3
⇔(x=2∧y=3)∨(x=-2∧y=3)
et donc S={(2;3) ; (-2;3)}.

Exercice tp

Résoudre le système suivant

{	x²-4 =	0
	(y-1)(y+3) =	0

3.2 Raisonnements mathématiques

3.2.1 Raisonnement par l’absurde

Pour montrer qu'une proposition q est vraie
il suffit de suivre les étapes suivantes.
1) On suppose que q est fausse
2) Après les étapes d'inférence..
on obtient une propostion p et sa négation ⌉p toutes les deux vraies et ce n'est pas possible.
3) On déduit que ce qu'on a supposé est faux et donc q est vraie.

Exemple
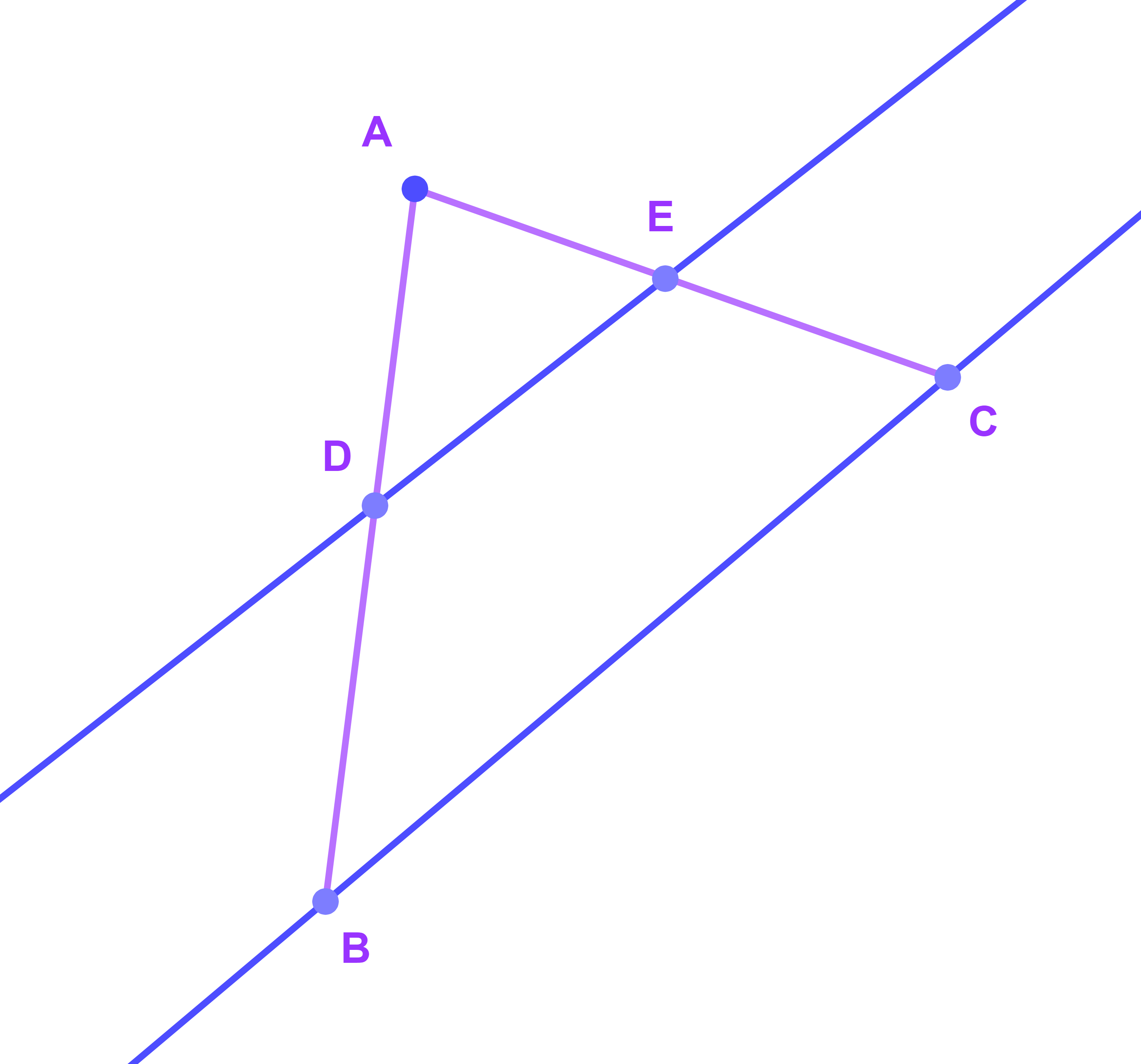
Soit ABC un triangle tels que AB=5,4 ; BD=3 ; CE=2,25 et AC=4,25 avec E∈[AC] et D∈[AB].
Est ce que (DE)||(BC) ?

Correction
On suppose que (DE)||(BC)

d'après le théorème de Thalès

AB	=	AC
BD		CE

Ou encore

5,4	=	4,25
3		2,25

ou encore 5,4.2,25=3.4,25
ou encore 12,15=12,75 et ce n'est pas possible donc la supposition est fausse
et par conséquent (DE) et (BC) ne sont pas parallèles.