Produit scalaire (6)
4- Positions relatives d’une sphère et un plan ou une droite
4.1 Intersection d’une sphère et un plan
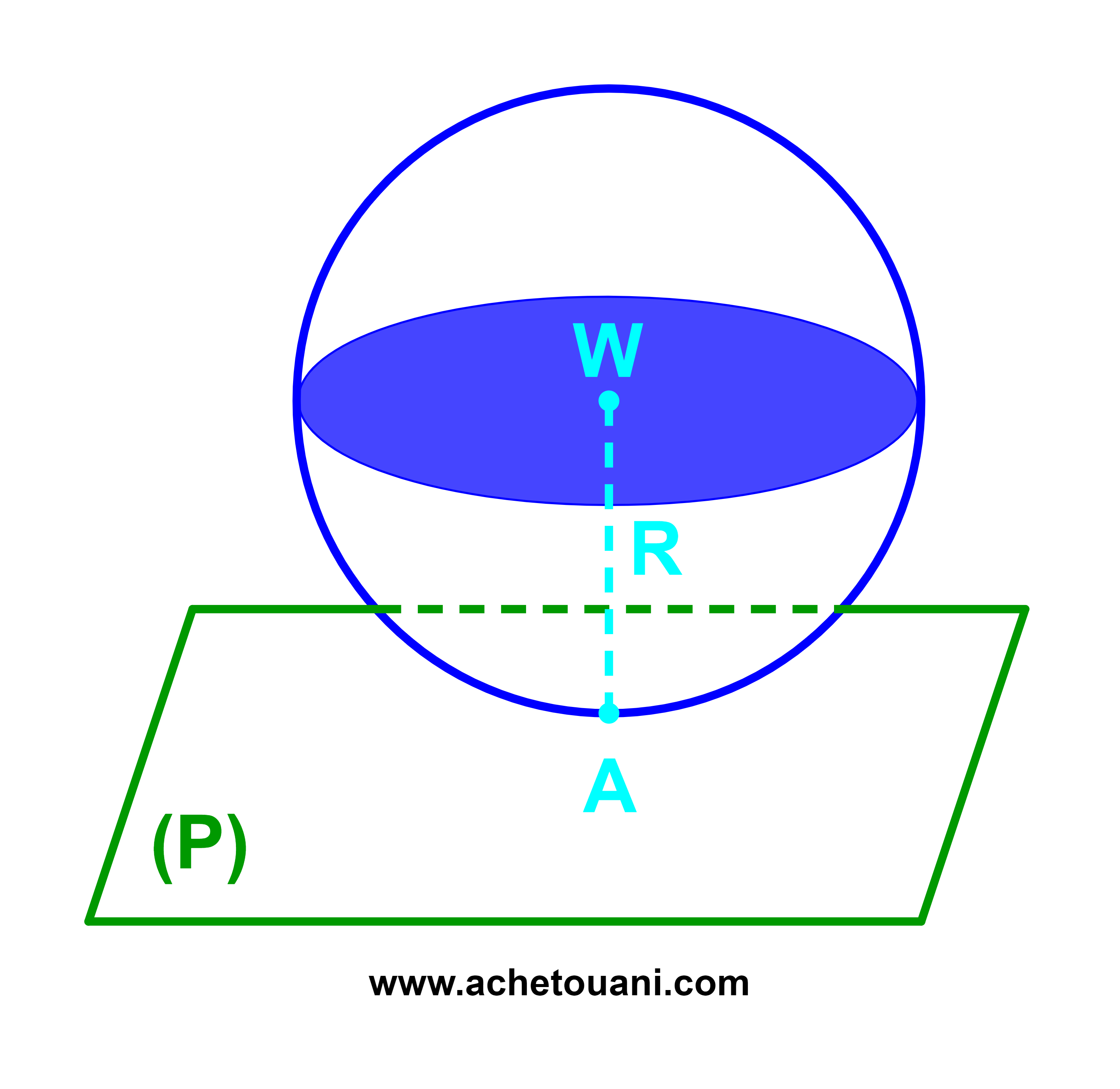
Soient (S) une sphère de centre W et de rayon R
et P un plan de vecteur normal n→.
Il existe 3 dispositions:
Si d(W;P) > R alors P∩S=∅.
Si d(W;P) = R le plan P est tangente à la sphère.
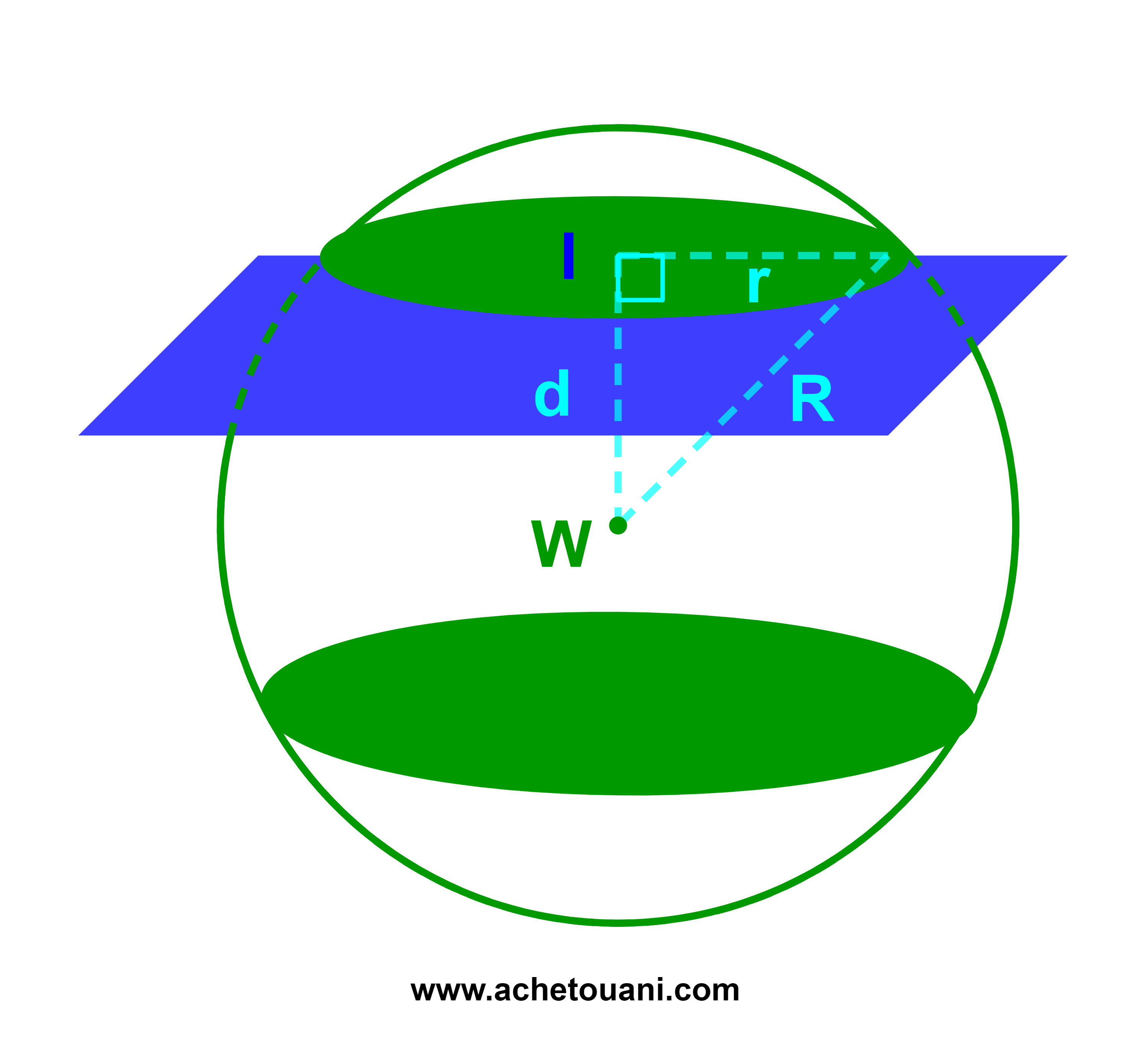
Si d(W;P) < R alors P coupe la sphère selon un cercle (C) de centre I avec P∩(WI)={I}.
n→ est un vecteur directeur de (WI).
Le rayon r du cercle (C) est défini par r²=R²-d²
( en utilisant le théorème de Pythagore ).
Exercice 1 tp
L'espace est rapporté à un repère orthonormé (O;i→;j→;k→).
Soit (S) une sphère de centre W(1;1;2) et de rayon R=2.
On considère un plan P d'équation 2x+y-z+2=0.
Déterminer la position relative de la sphère et le plan P.
Correction
On a d(W;P)=|2+1-2+2|/1 = 1 < 2 donc le plan P coupe la sphère selon un cercle (C) de rayon r=√(2²-1²)=√3.
Son centre I est déterminé en résolvant le système suivant
| I∈(P)∩(S) ⇔ | x=1+2t | t∈ ℝ |
| y = 1+t | ||
| z = 2-t | ||
| 2x+y-z+2=0 |
donc 2(1+2t)+1+t-2+t+2 = 0 ou encore
| t = | -1 |
| 3 |
Donc le centre du cercle (C) est défini comme suivant
| I( | 5 | ; | 4 | ; | 54 | ) |
| 3 | 3 | 3 |
4.2 Intersection d’une sphère et une droite
Soient S(Ω;R) une sphère et (D) une droite de vecteur directeur u→(α;β;γ)
il y'a 3 dispositions
Si d(Ω(D))>R alors (D) et (S) sont disjoints et on écrit (D)∩(S)=∅.
Si d(Ω(D))<R alors (D) coupe la sphère en deux points A et B.
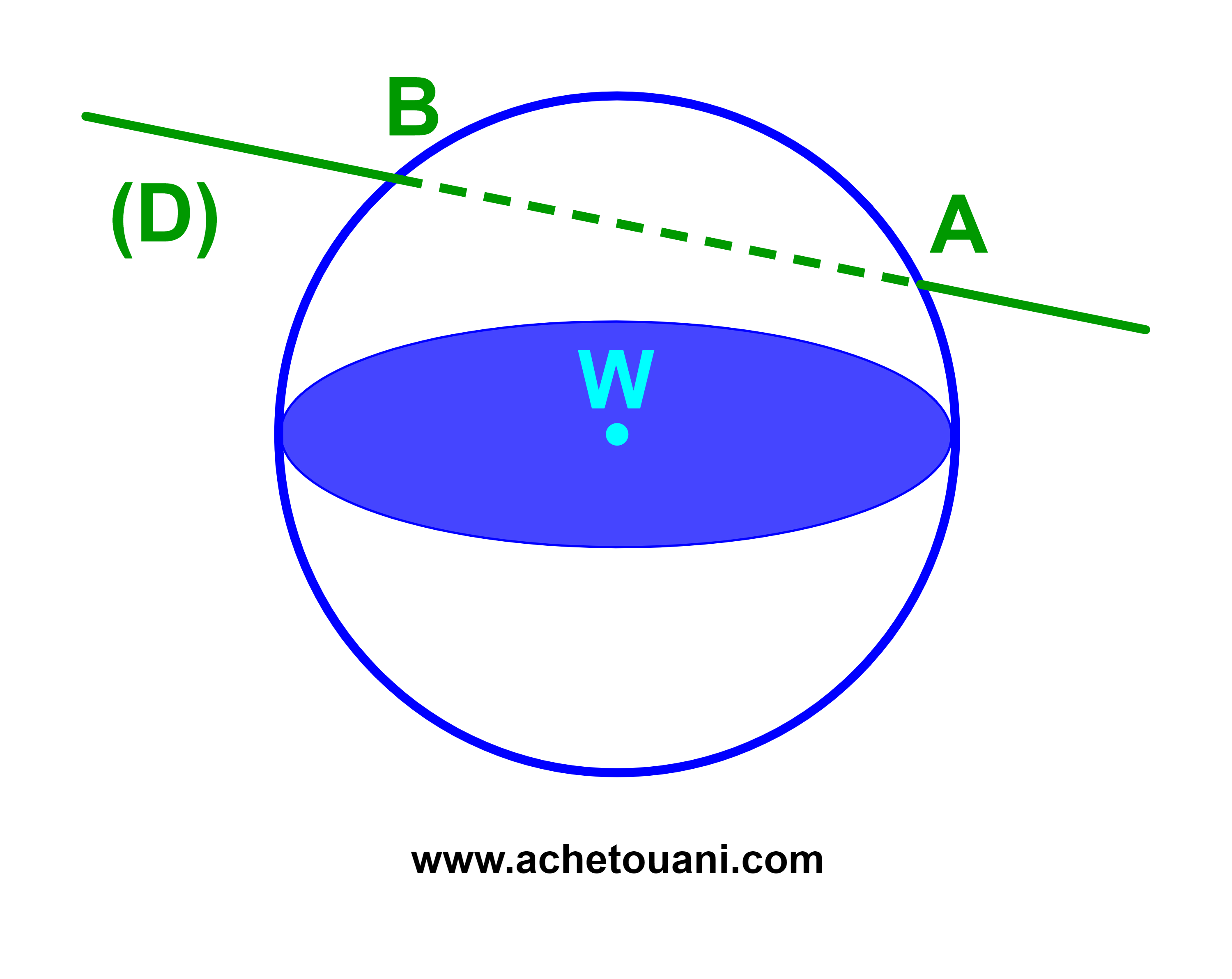
Pour déterminer A et B il suffit de résoudre le système suivant
| H∈(D)∩S ⇔ | x=xI+tα | t∈ ℝ |
| y = yI+tβ | ||
| z = zI+tγ | ||
| (x-a)²+(y-b)²+(z-c)²=R² |
Si d(Ω(D))=R alors (D) est tangente à la sphère en un seul point.
Notons qu'il suffit de résoudre le même système pour le déterminer.