Nombres complexes (3)
1.2 Plan complexe
1.3.1 Affixe d'un point et d'un vecteur
Définition 1
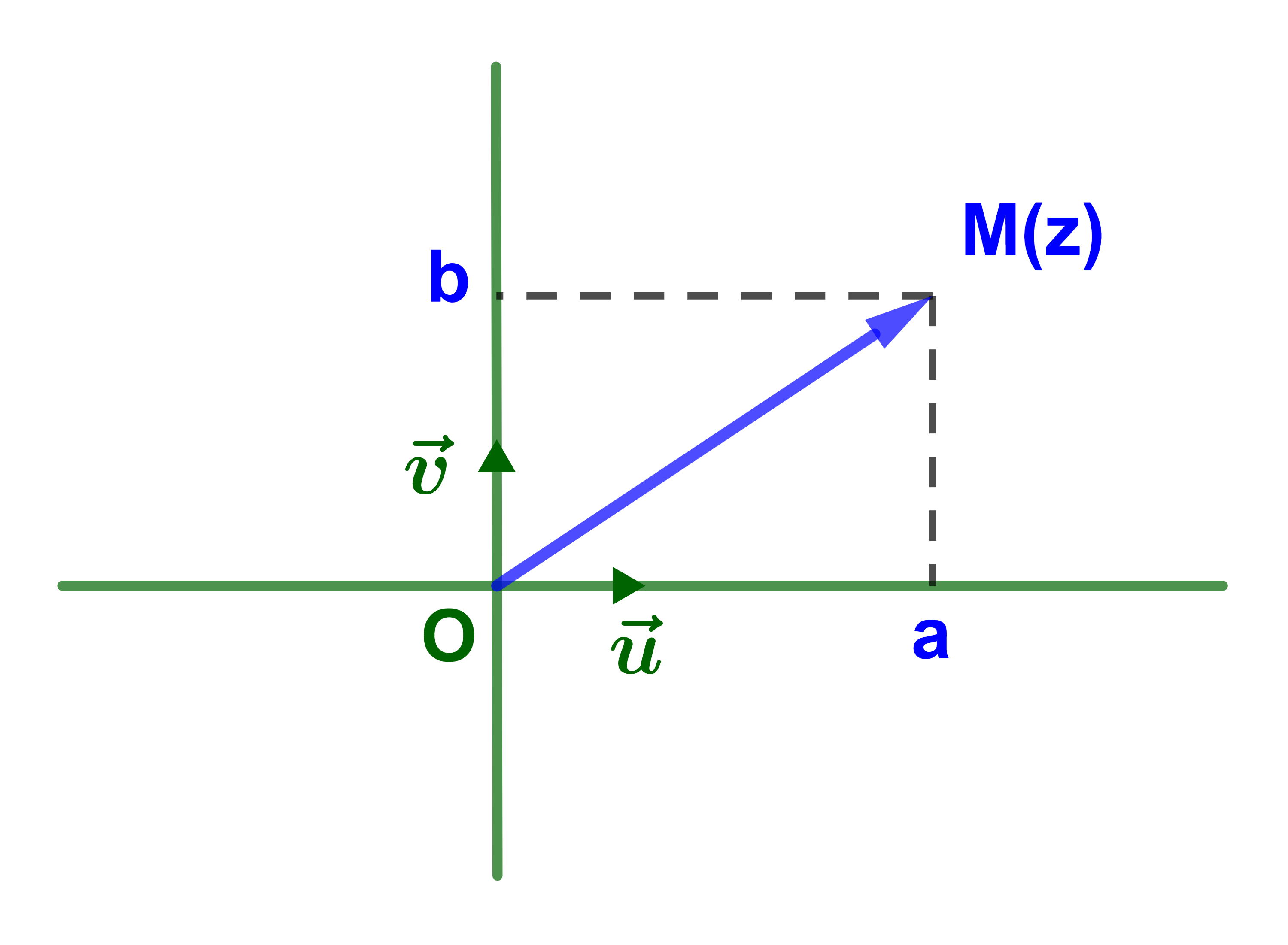
Le plan est rapporté à un repère orthonormé direct (O;u→;v→).
1) On associe chaque nombre complexe z=a+bi (tels que a;b∈IR) au point M(a;b)
appelé point image de z et le vecteur OM→ est appelé vecteur image de z.
Définition 2
Inversement, on associe chaque point M(a;b) du plan au nombre complexe z=a+bi
appelé l'affixe du point M
et aussi l'affixe du vecteur OM→.
La notation M(z) signifie que le point M ayant pour affixe z.
La notation zM signifie que z est l'affixe du point M.
Plan complexe
1) L'ensemble des points M(z) tel que (z∈ℂ) est appelé Plan complexe.
2) L'axe (O,u→) est appelé l'axe des parties réelles.
3) L'axe (O;v→) est appelé l'axe des parties imaginaires.
1.2.2 Affixe du vecteur AB→
Soient A(z) et B(z') deux points du plan complexe tels que z=x+yi et z'=x'+y'i avec x;y;x';y'∈IR
On a AB→=(x'-x)u→+(y'-y)v→ donc l'affixe du vecteur AB→ est x'-x+(y'-y)i
or x'-x+(y'-y)i=(x'+y'i)-(x+yi)=z'-z.
Propriété
Soient A(z) et B(z') deux points du plan complexe.
L'affixe du vecteur AB→
ZAB→ = z'-z.
Exemple
Soient A(-4+3i) et B(-1+5i) deux points.
Déterminer l'affixe du vecteur AB→.
Correction
aff(AB→)=(-1+5i)-(-4+3i)
=-1-(-4)+i(5-3)
ainsi aff(AB→)=3+2i.
1.3.3 Affixe du milieu d'un segment [AB]
I est milieu du segment [AB]
⇔ 2OI→=OA→+OB→
donc 2.aff(I)= z+z'.
Propriété
Soient A(z) et B(z') deux points.
L'affixe du milieu I de [AB] est défini par
| aff(I) = | z+z' |
| 2 |
Exemple
Soient A(7+3i) et B(-3+5i) deux points.
Déterminer l'affixe du milieu du segment [AB].
Correction
| aff(I) = | (7+3i)+(-3+5i) |
| 2 |
ainsi aff(I) = 2+4i.