Nombres complexes (4)
1.2 Conjugué d’un nombre complexe
1.2.1 Définition
Soit z=a+bi∈ℂ tel que a;b∈IR.
Le nombre complexe a-bi est appelé Conjugué du nombre complexe z et est noté z.
On écrit z = a+ib
ou encore z = a-ib.
Exemples
7+3i=7-3i et -2-i= -2+i.
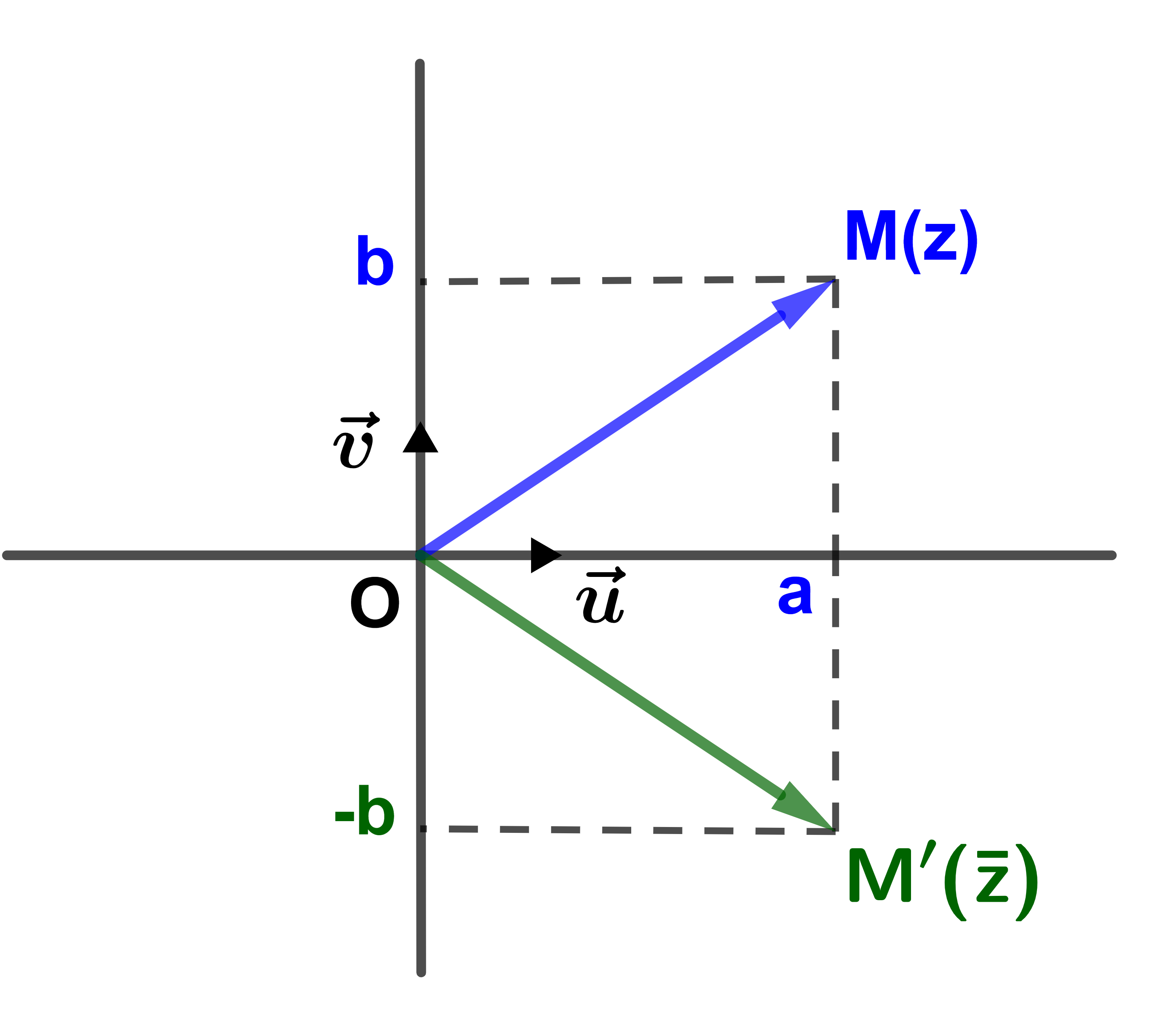
Réprésentation graphique
Soit z∈ℂ et M son point image.
On représente M'(z) tel que z est le conjugué de z.
1.2.2 Propriétés
Soient z et z' deux nombres complexes avec z'≠0
k∈IR et n∈ℤ.
| z+z' | = | z + z' | k.z | = | k.z | |
| z.z' | = | z.z' | z.z...z | = | (z)n |
| ( | 1 | ) = | 1 | ( | z | ) = | z | |
| z | z | z' | z' |
Exercice 1 tp
Sans déterminer la forme algébrique
donner le conjugué de z et de z'
sachant que z=(4-5i).(3+i)
| et z'= | 4-5i |
| 3+i |
Correction
z = (4-5i)(3+i) = (4-5i) × (3+i)
Donc z = (4+5i)(3-i).
| z'= | 4-5i | = | 4+5i |
| 3+i | 3-i |
1.4 Module d’un nombre complexe
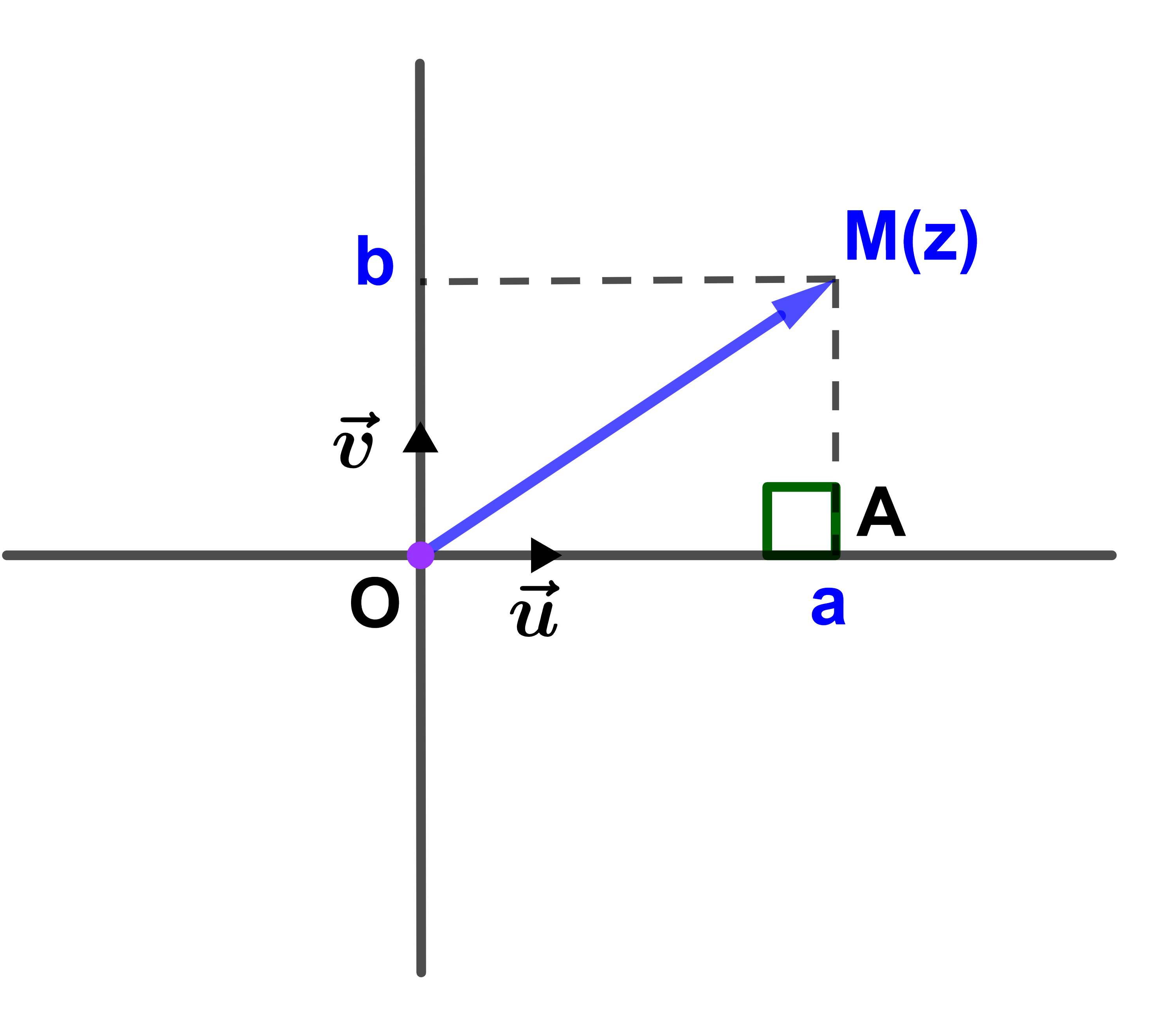
Dans le plan complexe rapporté à un repère orthonormé direct (O;u→;v→), on considère un point M(a;b) d'affixe z=a+ib avec a;b∈IR.
En utilisant le théorème de Pythagore appliqué au triangle rectangle OAM on obtient
OM² = a²+b² ou encore OM=√(a²+b²).
Et on a z.z=a²+b².
1.4.1 Définition
Soit z∈ℂ et M son point image.
Le module de z, noté |z| est la distance OM
ou encore |z|=√(zz) = √(a²+b²).
Exemples
| 5 + 3i | = √(5²+3²) = √(34)
|√2+i√7| = √((√2)²+(√7)²) = 3.
|1-√(3)i|= √(1²+(-√(3))²) = 2.
1.4.2 Propriétés
Soient z;z'∈ℂ avec z'≠0 ; k∈IR et n∈ℤ.
|-z| = |z| = |z|
|z.z'| = |z|.|z'|
| | | 1 | |= | 1 |
| z' | |z'| |
| | | z | |= | |z| |
| z' | |z'| |
|zn| = |z|n
|z + z'|≤|z|+|z'| (l’inégalité triangulaire).
Cas général
| | | k=n ∏ k=1 |
zk| | = | k=n ∏ k=1 |
|zk| | ||
| | | k=n ∑ k=1 |
zk | | | ≤ | k=n ∑ k=1 | |zk| |
Remarque
Si z∈IR alors le module de z est la valeur absolue de z.
Exemples
| 0 | = 0
| 13 | = 13
| -27 | = 27.