Nombres complexes (5)
1.5 Argument d’un nombre complexe non nul
Le plan complexe est rapporté à un repère
orthonormé direct (O;u→;v→).
1.5.1 Définition
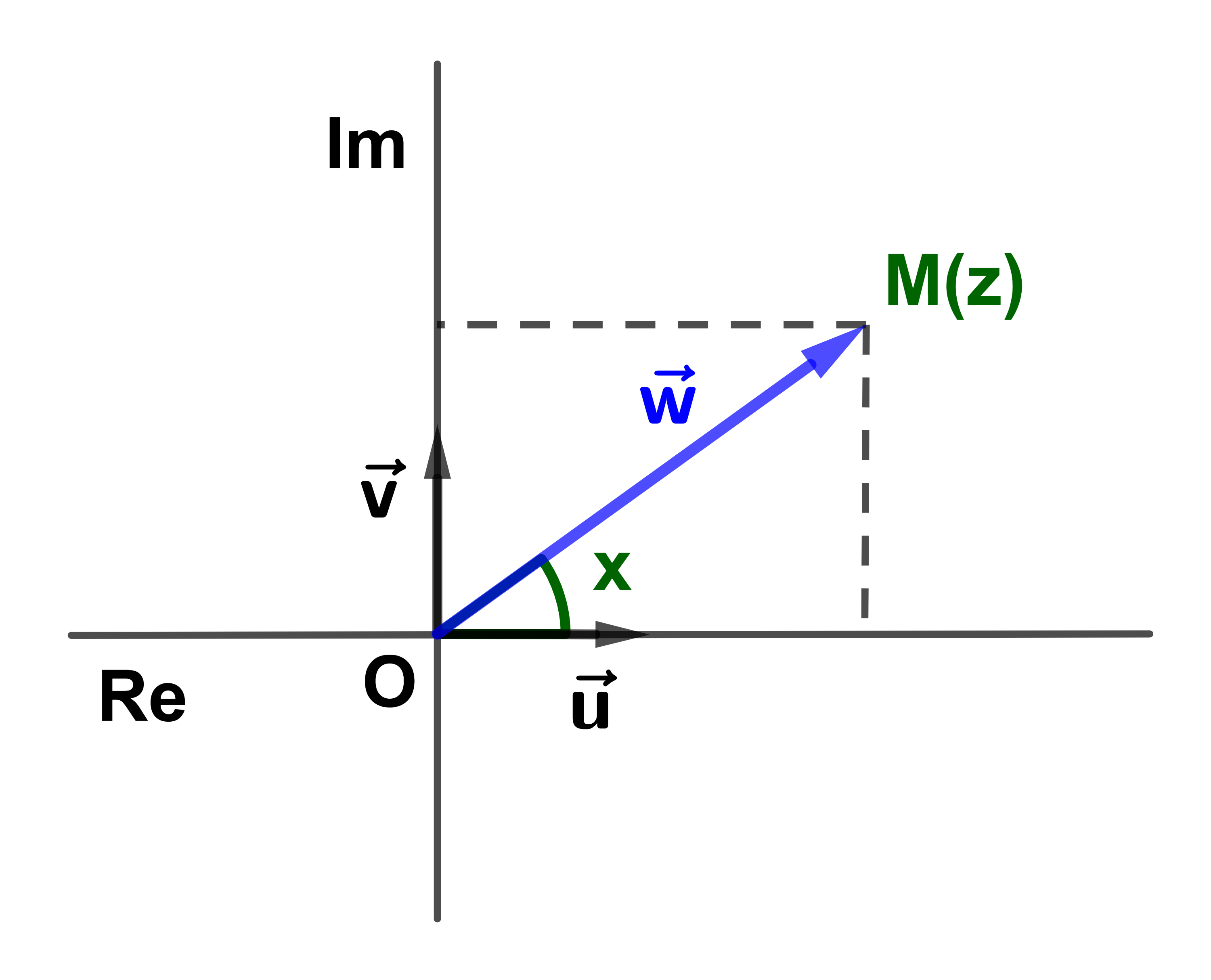
Soit z∈ℂ et M(z) son point image.
Une mesure exprimée en radians de l'angle (u→;OM→)
est appelée argument du nombre complexe z, noté arg z.
Si w→ est un vecteur image de z
alors
arg z = (u ; w)+2kπ avec k∈ℤ.
1.5.2 Propriétés
caractéristique d'un nombre réel
z∈IR ⇔ z=0 ou arg z= 0+kπ avec k∈ℤ.
caractéristique d'un imaginaire pur
z∈iIR ⇔ z=0 ou arg z=(π/2)+kπ avec k∈ℤ.
Remarque
0 n'a pas d'argument et il est considéré comme un imaginaire pur.
Propriétés
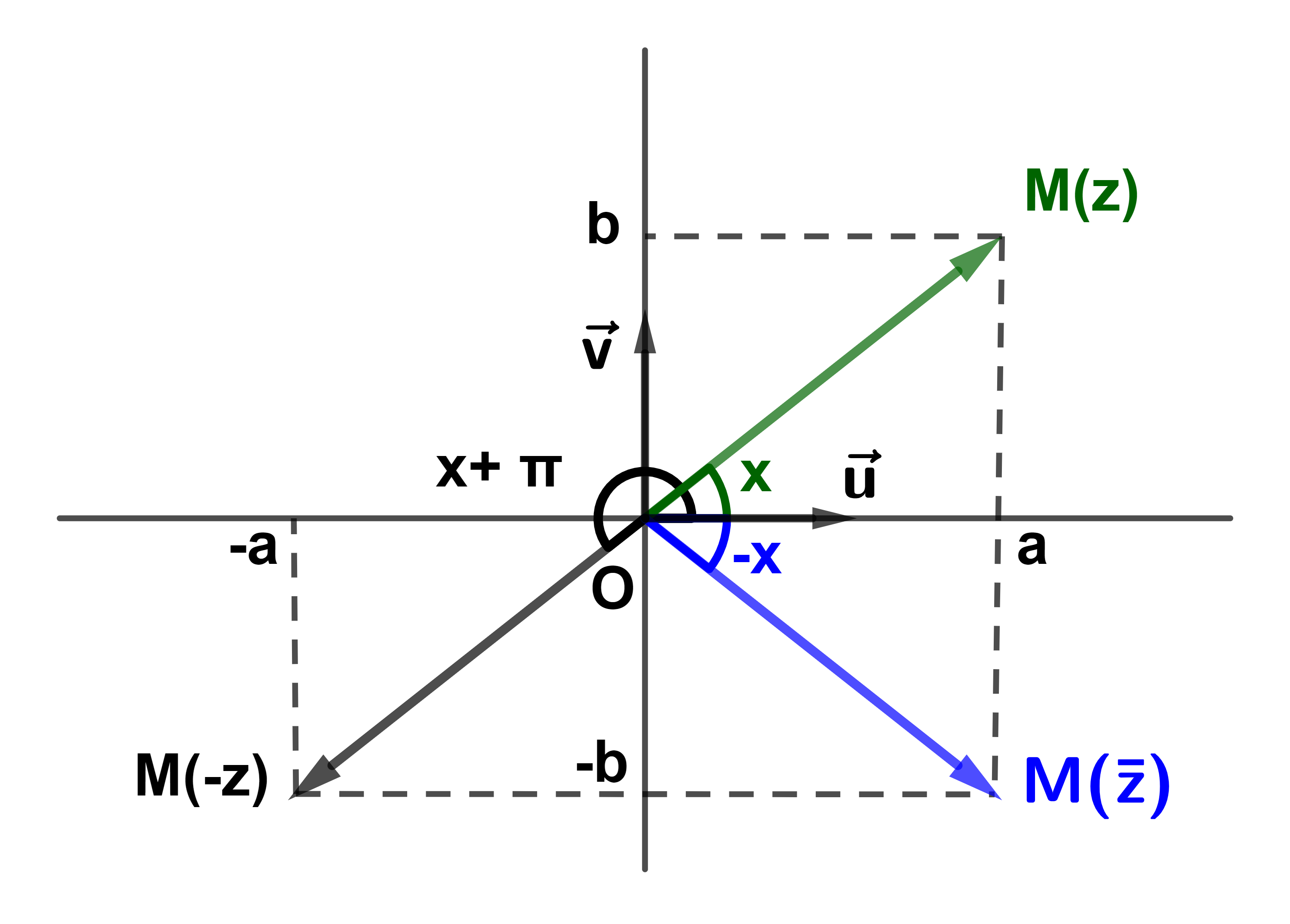
Soit z∈ℂ*
arg(z) = - argz+2kπ avec k∈ℤ.
arg(-z) = π+ argz + 2kπ avec k∈ℤ.
Propriétés
Soient z;z'∈ℂ* et n∈IN*.
z=z' ⇔ | z |=| z' | et argz ≡ argz'[2π]
arg(-z) = π+argz +2kπ avec k∈ℤ
argz= - argz +2kπ avec k∈ℤ
arg(z.z') = argz + argz' +2kπ avec k∈ℤ
arg(z.z...z) = n(argz) + 2kπ avec k∈ℤ.
| arg | 1 | = -argz'+2kπ avec k∈ℤ |
| z' |
| arg | z | = argz-argz'+2kπ avec k∈ℤ |
| z' |
Exemples
Soient z et z' deux nombres complexes tels que
| arg(z) = | π | + 2kπ avec k∈ℤ |
| 4 | ||
| arg(z') = | π | + 2kπ avec k∈ℤ |
| 3 |
Déterminer arg(-z); arg(z); arg(z.z')
| et arg | z |
| z' |
Correction
1) arg(-z) = π+argz +2kπ signifie
| arg(-z) = π + | π | +2kπ |
| 4 |
| Donc arg(-z) = | 5π | +2kπ avec k∈ℤ |
| 4 |
2) argz = - argz +2kπ signifie
| argz = | - π | +2kπ ; k∈ℤ |
| 4 |
3) arg(z.z') = argz + argz' +2kπ signifie
| arg(z.z') = | π | + | π | +2kπ |
| 4 | 3 |
| Donc arg(z.z') = | 7π | +2kπ |
| 12 |
| 4) arg | z | = argz-argz'+2kπ avec k∈ℤ |
| z' |
| Donc arg | z | = | - π | +2kπ avec k∈ℤ |
| z' | 12 |