Dérivation et représentation (12)
Exercice 1 tp
Soit f une fonction définie sur IR+ par
f(x) = |x² - 2|
et (C) sa courbe dans un repère
orthonormé (O ; i→ ; j→)
1) Montrer que f est paire et déterminer le domaine d'étude réduit de f
2) Etudier la dérivabilité de f au point √(2) et déterminer les demi tangentes de la courbe (C)
3) (a) Etudier la dérivabilité de f sur IR+\{√2}
puis étudier la monotonie de f sur IR+\{√2}.
(b) Tracer le tableau de variations de f sur IR
4) Tracer la courbe (C)
Correction
1) ∀x∈IR on a x²-2∈IR
donc |x²-2|∈IR ainsi D=IR
∀x∈IR on a (-x)∈IR
et f(-x) = |(-x) - 2| = |x² - 2| = f(x)
Et donc f est une fonction paire ainsi la courbe (C) est symétrique par rapport à l'axe des ordonnées
Alors le domaine d'étude réduit de f est IR+
2) f(√(2)) = 0
La dérivée à doite à √(2)
On a donc x≥√(2) et |x²-2| = x²-2
lim √(2) |
f(x)-f(√(2)) | = | lim √(2)+ | x²-2 |
| x-√(2) | x-√(2) |
| = | lim √(2)+ |
x+√(2) | = 2√(2) |
donc f est dérivable à droite à √(2) et f 'd(√(2))=2√(2)
2) La dérivée à gauche à √(2)
On a donc x≤√(2) et |x²-2| = -(x²-2)
lim √(2)- |
f(x)-f(√(2)) | = | lim √(2)+ |
-(x²-2) |
| x-√(2) | x-√(2) |
| = | lim √(2)- |
-x-√(2) = -2√(2) |
donc f est dérivable à gauche à √(2)
et f 'g(√(2))=-2√(2)
puisque f 'g(√(2))≠f 'd(√(2))
alors f n'est pas dérivable en √(2)
Mais f est dérivable à droite et à gauche à √(2)
et la courbe (C) admet une demi-tangente à droite A(√(2);0)
d'équation y=2√(2)x-4
et une une demi-tangente à gauche A(√(2);0)
d'équation y=-2√(2)x+4
3) (a) Soit x∈IR+\{√2}
f(x)=|x²-2| on peut écrire f(x) sans valeur absolue en étudient le signe de x²-2
| x | 0 | √2 | +∞ | |||
| x²-2 | - | 0 | + |
Donc
| { | f(x) = | -x² + 2 | si 0≤x≤√2 |
| f(x) = | x² - 2 | si x≥√2 |
La restriction de f sur l'intervalle I=[0 ; √2[ est une réstriction d'un polynôme donc f est dérivable sur I
Soit x∈I on a f '(x) = (-x²+2)' = -2x
La restriction de f sur l'intervalle J=]√2 ; +∞[ est une réstriction d'un polynôme donc f est dérivable sur J
Soit x∈J on a f '(x) = (x²-2)' = 2x
Notons que f '(0)=0
Alors f est dérivable sur IR+\{√2}
Monotonie de f sur I
Soit x∈I\{0} on a -2x<0 donc f'(x)<0 ainsi f est strictement décroissantes sur I
Monotonie de f sur J
Soit x∈J on a 2x>0 donc f'(x)>0 ainsi f est strictement croissantes sur J
Tableau de variations de f sur IR
f est strictement décroissantes sur I et puisque f est paire alors f est strictement croissante
sur ]-√2 ; 0]
f est strictement croissantes sur J et puisque f est paire alors f est strictement décroissante
sur ]-∞ -√2[
| x | -∞ | - √2 | 0 | √2 | +∞ | |||||
| f ' | - | || | + | 0 | - | || | + | |||
| f | +∞ | ↘ |
0 |
↗ |
2 | ↘ |
0 |
↗ | +∞ |
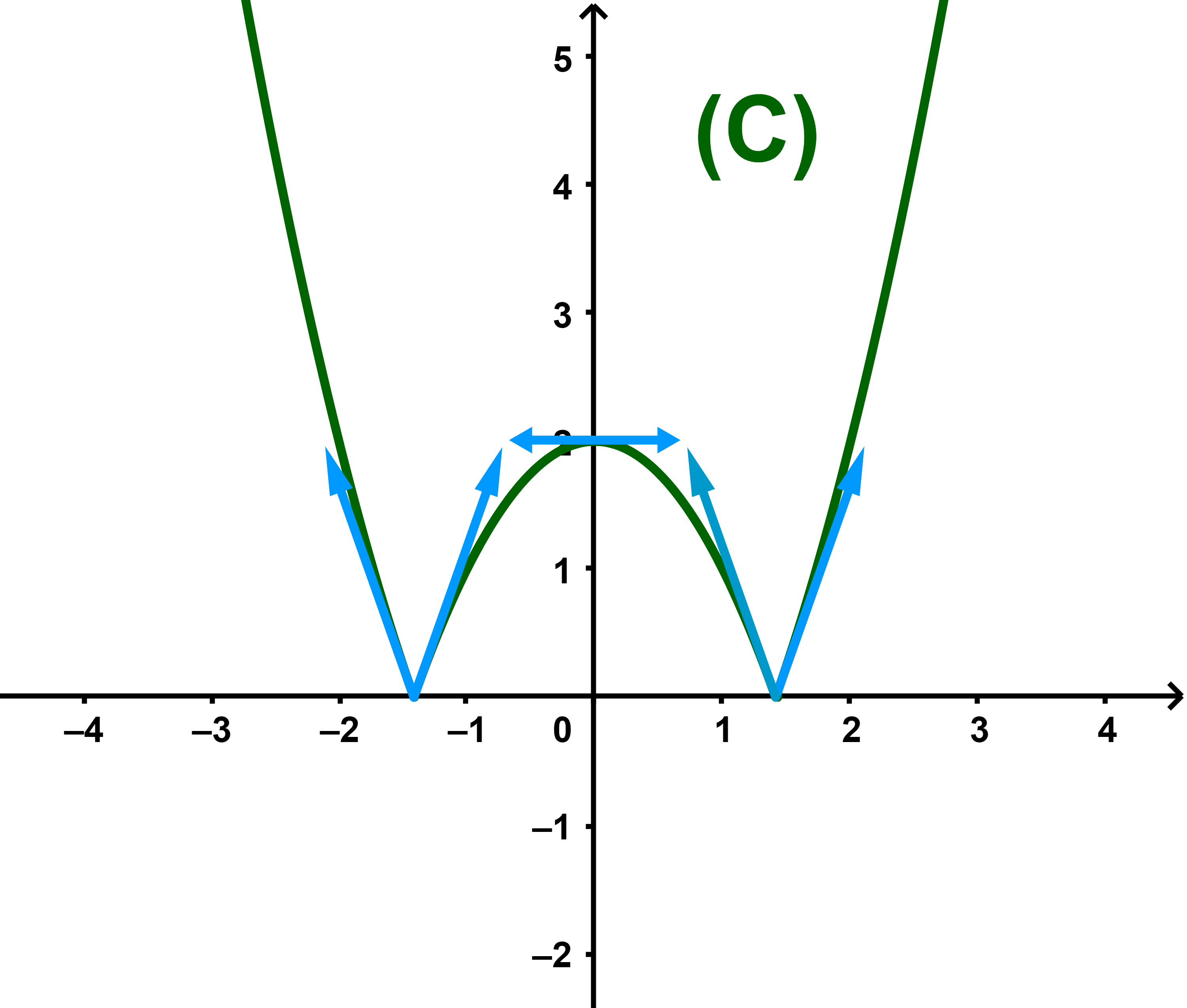
4) La courbe (C)
Notons que f est paire donc (C) admet deux demi-tangentes au point B(-√(2);0)
de plus elle admet une tangente au point d'abscisse 0
d'équation y=0(x-0)+f(0)=2