النهايات والاتصال (3)
تمرين
لتكن g دالة معرفة كما يلي :
g(x)= √(x²-1)-x ;
ادرس اتصال g على Dg
8.2 خاصية (نهاية مركب دالة متصلة و دالة تقبل نهاية )
لتكن f دالة معرفة على مجال I و g دالة معرفة على مجال J يتضمن f(I) ;
اذا limaf(x)= L و g متصلة في L
فان limagof(x)=g(L)
تمرين
لتكن f دالة عددية معرفة كما يلي
| lim4f(x) احسب | f(x)=√( | x²-16 | ) |
| x-4 |
9- مبرهنة القيم الوسيطة
9.1 مبرهنة
لتكن f معرفة ومتصلة على I=[a;b], a < b و m=minf(x) و M=maxf(x) لدينا
∀k∈[m;M])(∃x∈I): f(x)=k
وبتعبير آخر :
لكل عدد حقيقي k محصور بين f(a) و f(b), المعادلة f(x)=k
تقبل حلا على الاقل في المجال[a;b]
9.2 لازمة لمبرهنة القيمة الوسيطة
لتكن f دالة عددية متصلة ورتيبة قطعا على المجال [a;b], a< b
لكل عدد حقيقي k, محصور بين f(a) و f(b) المعادلة f(x)=k تقبل حلا وحيدا في المجال [a;b]
9.2.1 ملاحظة :
اذا f غير معرفة في a او في b , المبرهنة تبقى صحيحة باعتبار النهاية في a او في b.
9.2.2 نتيجة 1
اذا f متصلة على I=[a;b] و f(a).f(b) < 0 فان المعادلة f(x)= 0 تقبل حلا على الاقل في المجال I.
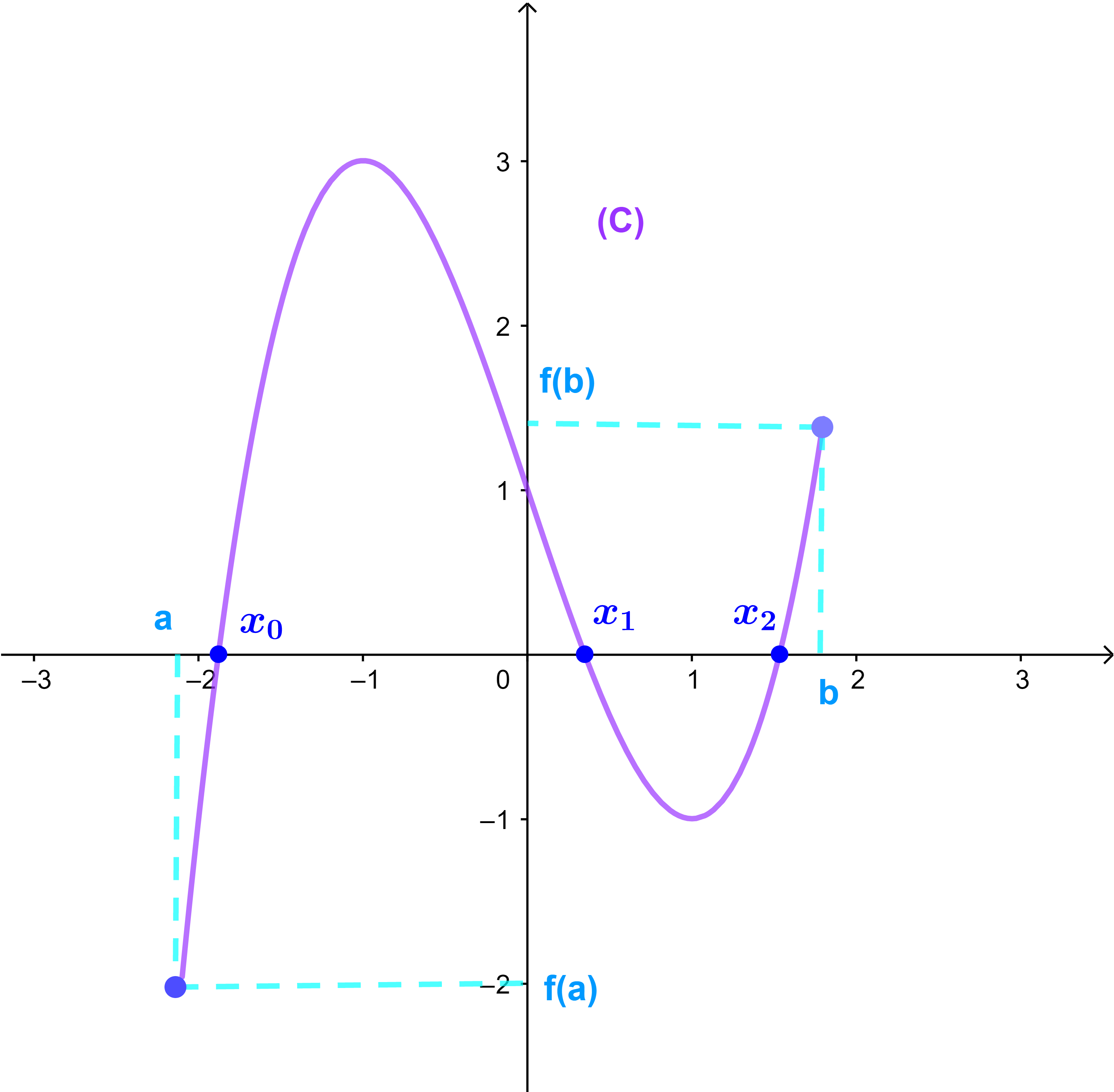
9.2.3 نتيجة 2
واذا f متصلة ورتيبة قطعا على المجال I و f(a).f(b) < 0 فان المعادلة f(x)= 0 تقبل حلا وحيدا x0 في I
بحيث a< x0< b
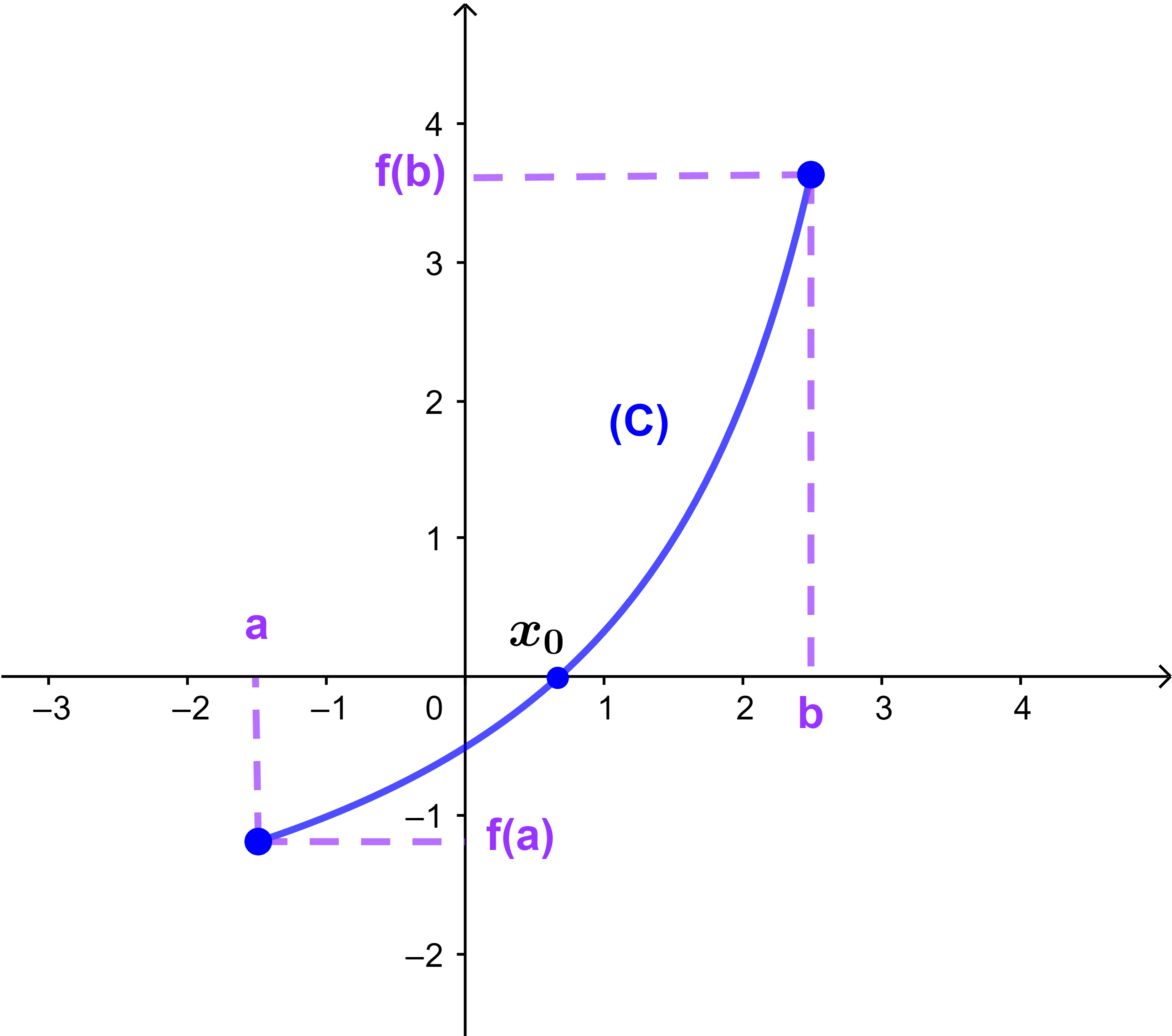
تمرين
بين ان المعادلة x-cosx=0 تقبل حلا وحيدا في المجال
I=]π/6 ; π/4[
تمرين طريقة التفرع الثنائي
لتكن f دالة معرفة كما يلي
f(x)=x³-4x²+4x-1
بين ان المعادلة f(x)=0 تقبل حلا وحيدا a في المجال I=]2;3[
حدد تأطيرا للعدد a سعته 0,25
باستعمال طريقة التفرع الثنائي
تصحيح
لدينا f دالة حدودية اذن متصلة وقابلة للاشتقاق على IR
f'(x)=3x²-8x+4, ندرس اشارة f'
| x | -∞ | 2/3 | 2 | +∞ | |||
| f'(x) | + | 0 | - | 0 | + |
[2;3]⊂[2;+∞[ اذن f تزايدية قطعا على [2;3] وبما ان f متصلة على IR فان f متصلة على [2;3] وحسب T.V.I ∃!a∈[2;3], f(a)=0 اي المعادلة f(x)=0 تقبل حلا وحيدا في المجال I=[2;3]
لدينا مركز المجال I هو
2,5
اذن a∈[2; 2,5] او a∈[2,5 ;3]
لدينا f(2,5)=-0,375<0 و f(3)>0 وحسب TVI, a∈J=]2,5 ;3[; (سعته 3-2,5=0,5)
نواصل
مركز المجال J
هو
2,75 و f(2,75)=0,54.. >0 اذن a∈]2,5 ;2,75[ (سعته 2,75-2,5=0,25)
اذن
]2,5 ;2,75[ تأطير للعدد a سعته
0,25
10- مبرهنة الدوال العكسية (مبرهنة الدوال التقابلية )
10.1 مثال
لتكن f دالة معرفة على IR+ بما يلي : f(x)=x²
لدينا f قصور دالة حدودية اذن متصلة على IR+
∀ x ; y ∈IR+: x < y ⇒ x² < y²
⇒ f(x) < f(y)
اذن f تزايدية قطعا على IR+
لدينا f(2)=4 اذن
4 صورة
2 بواسطة الدالة f و
2 هو الصورة العكسية للعدد
4 ونرمز له ب f-1(4)=2
لدينا f(7)= 49 اذن f-1(49)=7
10.2 مبرهنة وتعريف
اذا f متصلة ورتيبة قطعا على مجال I فانه توجد دالة وحيدة تسمى الدالة العكسية ونرمز لها ب f-1 ومعرفة على J=f(I) نحو I بما يلي :
| f-1(x)=y x∈J=f(I) | <=> | f(y)=x y∈I |
|---|
10.3 خاصية دالة تزايدية قطعا على مجال
اذا كانت f دالة عددية معرفة على مجال I وتحقق الشرطين التاليين :
c1. f متصلة على I
c2. الدالة f رتيبة قطعا على I.
فان :
. J=f(I) هو كذلك مجالا
. f تقابل من I نحو J اي تقبل دالة عكسية من J نحو I
. الدالة العكسية f-1 هي كذلك دالة متصلة على المجال I ورتيبة قطعا على I ولها نفس التغيرات .(اي اذا f تزايدية قطعا فان f-1 هي كذلك تزايدية قطعا I ..)
. Cf و Cf-1 متماثلان بالنسبة للمنصف الاول للمعلم اي المستقيم الذي معادلته y = x
11- دالة الجذر من الرتبة n لدالة موجبة
11.1 مثال
لتكن f دالة معرفة على IR+ ب : f(x)=x³
f متصلة وتزايدية قطعا على IR+ اذن تقبل دالة عكسية f-1 معرفة على IR+ ونكتب x -> ∛x وتسمى دالة الجذر المكعب للعدد x
11.2 تعريف
لتكن n∈IN* الدالة العكسية x->xn المعرفة على IR+ تسمى دالة الجذر من الرتبة n ونرمز لها ب n√x
11.3 خاصية
لتكن x و y عددين موجبين و n و m عددين طبيعيين وغير منعدمين
n√(xy)=n√x . n√y
(n√x)m=n√xm
n√xn=(n√x)n = x
بالاضافة اذا كان y>0 فان
| n√x | = n√( | x | ) |
| n√y | y |
n√x < n√y ⇔ x< y
n√m√x = nm√x
برهان
nm√x = y ⇔
x = ynm ⇔ x=(yn)m
⇔ yn = m√x ⇔ y=n√(m√x)
تمارين
بسط 3√125 ; 3√(8/27) ; 4√(81.16) ; √(3√81)
رتب الاعداد التالية : √2 ; 3√3 ; 4√4 ; 6√6
اجعل مقام كل من الاعداد التالية عددا جذريا
| 1 | ; | 1 |
| 3√2 +1 | 3√5 - 3√2 |