Signin
Mathématiques du secondaire qualifiant

Suites numériques (2)

2- Limite d'une suite

2.1 Limite finie d’une suite

2.1.1 Activités

Exemple 1
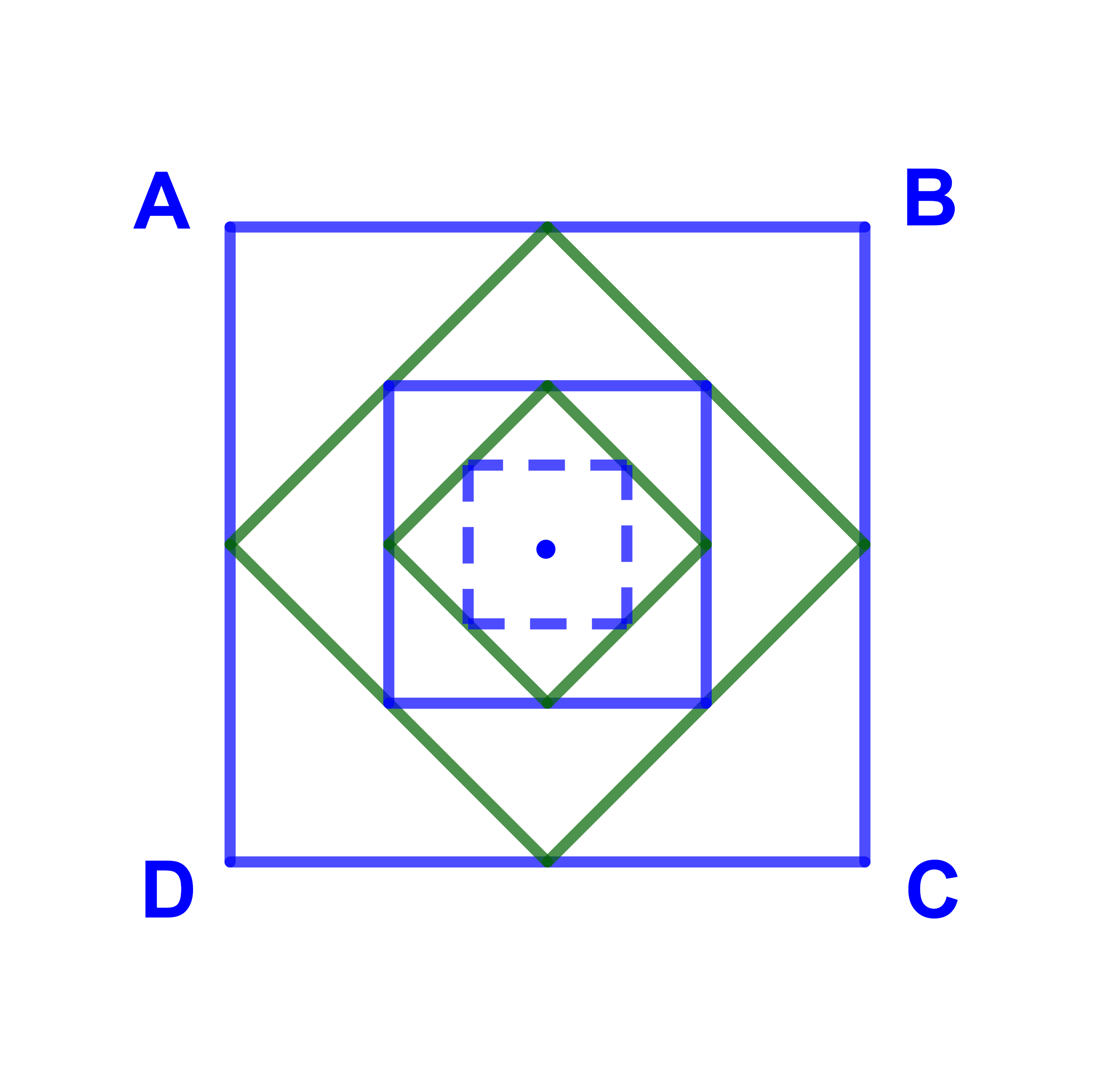
Soient C0 =(ABCD) un carré de surface S0=1.
C1 le carré de surface S1 et de sommets les milieux des cotés de C0 ...
et Cn le carré de surface Sn et de sommets les milieux des cotés de Cn-1.

Carré C0 C1 C2 .. Cn
Indice 0 1 2 .. n
Surface 1 1 1 .. 1
4 4² 4n-1

(Sn) est une suite géométrique de raison 1/4.
Quand n prend une grande valeur le carré est proche devenir un point donc la surface est proche de 0
on dit que la limite de la suite (Sn) est égale à 0.

On écrit
lim
+∞		(Sn) = 0

Exemple 2
Compléter le tableau suivant

n 10² 10³ 104 ... +∞
1 0,01 .. .. .. 0
n
1 0,0001 .. .. 0
n²
n 10² 10³ 104 ... +∞
1 .. .. .. .. 0
n³
1 0,1 .. .. .. 0
√n
1 .. .. .. .. 0
np

Plus la valeur n est élévée, plus la valeur du terme général diminue et tend vers 0.

2.1.2 Définition

Une suite (un) admet pour limite 0 si tout intervalle ouvert contenant 0, contient tous les termes de la suite à partir d'un certain rang.

on écrit
lim
+∞		 (un)n∈I = 0

autre définition


lim
+∞		 (un)n∈I
= 0 ⇔ (∀ε>0)(∃N∈IN)(∀n≥N):
un∈]-ε;+ε[

Résultat


lim
+∞		 (un)n∈I = L ⇔
lim
+∞		 (un)n∈I -L= 0
2.1.3 Théorème de l'unicité de la limite

Si une suite numérique admet une limite finie alors cette limite est unique.

Démonstration On suppose que la suite (un)n∈I admet deux limites L et L' (L < L')


lim
+∞		(un)n∈I
= L ⇔ (∀ε>0)(∃N∈I)(∀n≥N)
|un - L| < ε

lim
+∞		 (un)n∈I
= L' ⇔ (∀ε>0)(∃N'∈I)(∀n≥N')
|un - L'|<ε

On pose M=inf(N ; N')
donc (∀ε>0)(∃M∈I)(∀n≥M):
|un - L|<ε et |un - L'|<ε
|L - L'|= |L - un + un - L|
≤ |un - L| + |un - L'|<2ε

on pose ε = L + L'
2

donc L - L < L - L' et ce n'est pas possible ainsi L=L'.