Suites numériques (9)
2.5 Suites adjacentes
2.5.1 Définition
Soient (un)n∈I et (vn)n∈I deux suites numériques
on dit que (un)n∈I et (vn)n∈I sont adjacentes si les conditions suivantes sont vérifiées
1) (un)n∈I est croissante.
2) (vn)n∈I est décroissante.
| 3) | lim +∞ |
(un-vn) = 0 |
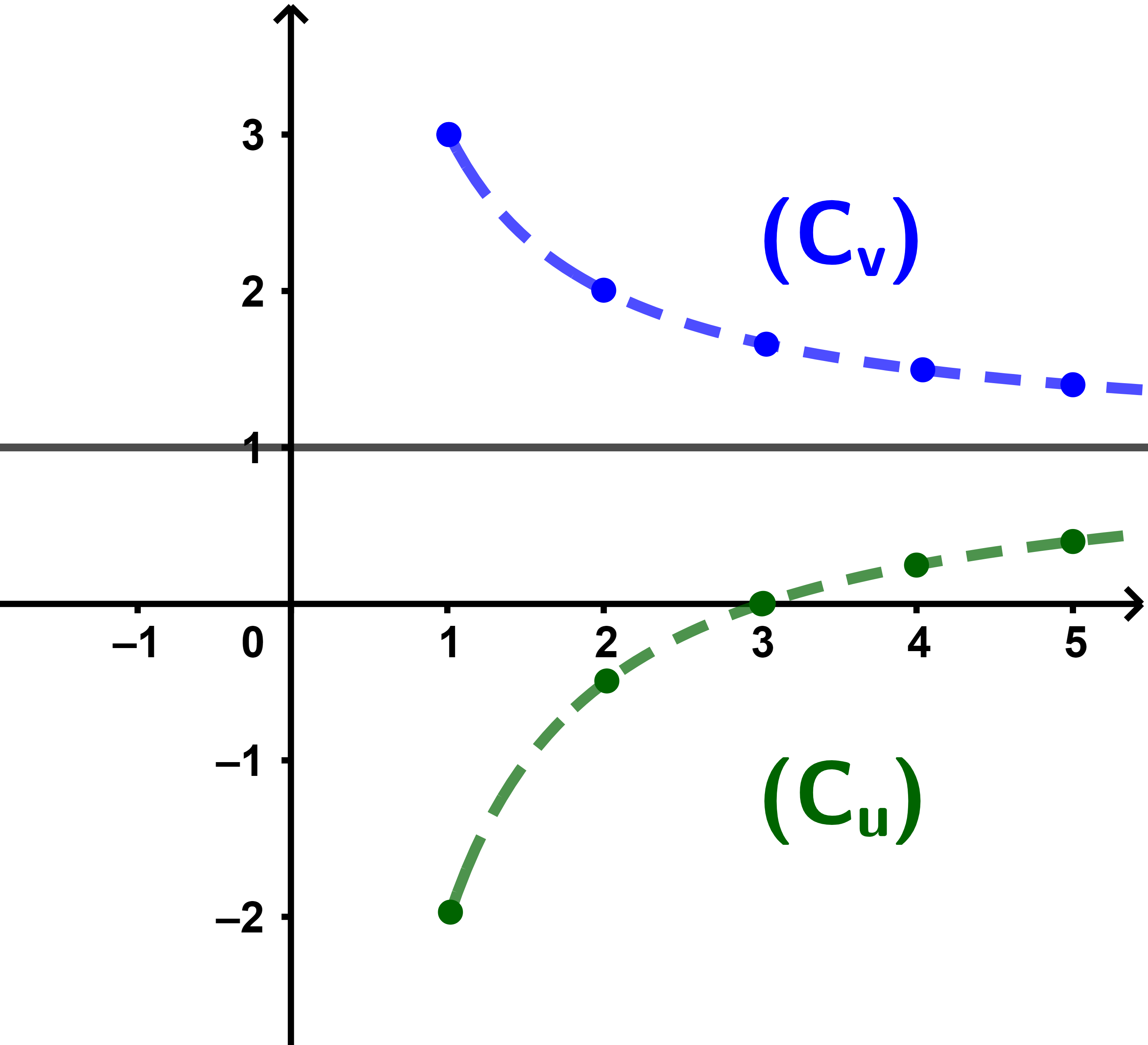
Exemple
Soit (un)n∈IN* et (vn)n∈IN* deux suites définies par
| un = | n-3 | vn = | n+2 | |
| n | n |
1) La suite (un)n∈IN* est croissante car ∀n∈IN*
| un+1 - un = | n+1 -3 | - | n-3 |
| n+1 | n |
| = | n²-2n -(n²-2n-3) | = | 3 |
| (n+1)n | (n+1)n |
puisque n∈IN* alors n+1>0 donc n(n+1)>0
ainsi un+1 - un > 0
2) La suite (vn)n∈IN* est décroissante car ∀n∈IN*
| vn+1 - vn = | n+1 + 2 | - | n+2 |
| n+1 | n |
| = | n²+3n - (x²+3n+2) | = | - 2 |
| n(n+1 | n(n+1) |
puisque n∈IN* alors n+1>0 et donc n(n+1)>0
-2<0 alors vn+1-vn<0
3) On pose wn=un-vn.
| wn = | n-3 | - | n+2 |
| n | n | ||
| = | n-3 - (n+2) | = | - 5 |
| n | n |
| lim +∞ |
- 5 | = 0 ⇒ | lim +∞ |
wn = 0 |
| n |
alors les suites (un)n∈IN* et (vn)n∈IN* sont adjacentes.
2.5.2 Propriété
Toutes suites réelles adjacentes (un)n∈I et (vn)n∈I sont convergentes et admettent la même limite L
et de plus (∀n∈I): un≤L≤vn.
Démonstration
On utilise le Théorème Fondamental de la convergence d'une suite
Toute suite croissante et majorée est convergente.
Toute suite décroissante et minorée est convergente.
1) La suite (un)n∈I est croissante donc il suffit de montrer qu'elle est majorée.
| lim +∞ |
(un-vn) = 0 ⇔ |
(∀ε>0)(∃N∈I)(∀n>N)⇒ |(un-vn)|<ε
⇒ -ε + vn<un<ε+vn
Puisque la suite (vn) est décroissante alors ∀n∈I={n∈IN/n≥p et p∈IN}: vn<vp.
Donc (∀n∈I): un<ε+vp
et donc ∃(M=ε+vp)(∀n∈I): un<M et cela signifie que la suite (un) est majorée.
La suite (un) est donc croissante et majorée alors elle est convergente vers un nombre L.
2) La suite (vn)n∈I est décroissante donc il suffit de montrer qu'elle est minorée.
On a
(∀ε>0)(∃N∈I)(∀n>N)⇒|(vn-un)|<ε
⇒ -ε+un<vn<ε + un.
Puisque la suite (un) est croissante
alors ∀n∈I={n∈IN/n≥p et p∈IN}: un>up
donc (∀n∈I): vn>up - ε
et donc ∃(M'=vp - ε)(∀n∈I): un>M' et cela signifie que la suite (un) est minorée
alors la suite (vn) est décroissante et minorée et donc convergente vers un nombre L'.
3) On montre que L=L' en utilisant les opérations sur les limites des suites convergentes.
| On a | lim +∞ |
(un-vn) = 0 |
| ⇔ | lim +∞ |
(un) - | lim +∞ |
(vn) = 0 |
| ⇔ | lim +∞ |
(un) = | lim +∞ |
(vn) |
ainsi L = L'
4) On montre que (∀n∈I): un≤L≤vn.
(a) On montre d'abord un≤vn.
On suppose par l'absurde que
(∃N∈I): uN>vN
donc uN - vN>0.
On pose η = uN - vN>0
puisque (un) est croissante alors
(∀n ≥ N ): un≥uN
et on a (vn) est décroisante alors
(∀n ≥ N): vn≤vN
Ou encore -vn≥-vN
donc (∀n ≥ N): un - vn ≥ uN - vN.
On a η>0 donc (∀n ≥ N): un-vn≥η>0
| On a | lim +∞ |
(un-vn) = 0 |
⇔ (∀ε > 0) (∃N'∈I)(n > N'): |un-vn| < ε
| on pose | ε = | η |
| 2 |
On obtient (∀n≥N): |un-vn| ≥ η > ε et ce n'est pas possible
ainsi (∀n∈I): un ≤ vn.
(b) La suite (un) est une suite croissante et majorée donc
| (∀n∈I): un ≤ | lim +∞ |
(un) |
ainsi (∀n∈I): un≤L.
La suite (vn) est une suite décroissante et minorée donc
| (∀n∈I): vn≥ | lim +∞ |
(vn) |
ainsi (∀n∈I): vn ≥ L
finalement (∀n∈I): un≤L≤vn.